Циркуляция магнитного поля

МАГНИТНОЕ ПОЛЕ

Основные понятия.

Компас был известен давно, но магнитное поле ввели и стали исследовать после открытия Эрстеда. Он обнаружил, что проводник с током оказывает влияние на компас. Магнитное поле обозначается . Эта величина называется индукцией магнитного поля (МП). Поскольку величина магнитного поля определяется через силу, действующую на контур с током, то магнитное поле является силовой характеристикой. Следовательно, его можно изображать с помощью силовых линий. Они называются линиями магнитной индукции. Вектор, касательный к этой линии, есть магнитная индукция. Он задает направление МП, а его величина равна значению магнитной индукции в точке касания. Было обнаружено, что магнитное поле оказывает влияние только на движущиеся заряды. Таким образом, магнитное поле действует на проводник с током. Это действие также зависит от формы и расположения проводников с током и направления тока. Оказалось, что рамка с током ведет себя подобно магнитной стрелке. С ней можно связать магнитный момент. Тогда взаимодействие рамки с током и внешнего магнитного поля можно рассматривать взаимодействие магнитного момента с магнитным полем. Если контур с током плоский, магнитный момент такого контура равен . 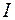= ток в контуре, 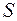- площадь контура. Магнитный момент во внешнем магнитном поле будет выстраиваться по полю. Это означает, что на него действует вращающий момент. 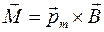. Направление магнитного поля проводника с током определяется правилом правого винта. Источником магнитного поля могут служить постоянные магниты. Они изготавливаются из специальных соединений, которые называются ферромагнетиками. Магнитное поле постоянного магнита можно наблюдать с помощью железных опилок. Поскольку контур с током создает свое магнитное поле, то движущиеся электроны в атомах и молекулах также создают магнитные поля. Эти токи были названы микроскопическими или молекулярными токами в отличие от внешних токов, которые называются макроскопическими. Магнитная индукция есть сумма вкладов от всех токов. Эта идея Ампера о молекулярных токах послужила основой для введения ещё одной характеристики – напряженности магнитного поля. Напряженность МП связана с магнитным полем макротоков. Связь индукции и напряженности магнитного поля

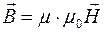
где - магнитная постоянная, 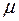- магнитная проницаемость среды. Она показывает, во сколько раз магнитное поле макротоков 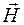изменяется за счет поля микротоков. Поскольку магнитная индукция является силовой характеристикой, она удовлетворяет принципу суперпозиции: . Единица измерения магнитной индукции – тесла.

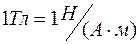. Единица напряженности магнитного поля – ампер на метр. .

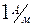Закон Био – Савара был установлен экспериментально. Их результаты были обобщены Лапласом. Для элемента с током этот закон в дифференциальной форме имеет вид:

,

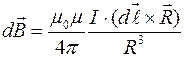где .

Рис.

В интегральной форме индукция МП, создаваемая линейными токами, равна

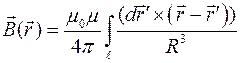
Вычисление этого интеграла в замкнутой форме не всегда возможно. Однако если контуры с током обладают симметрией, то подынтегральное выражение упрощается.

Закон Ампера

Ампер, исследуя влияние магнитного поля на проводник с током, установил, что сила, действующая на элемент тока равна

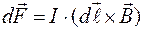, (1)

где 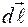элемент проводника с током 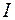. Направление вектора 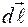совпадает с направлением тока. - индукция МП. Направление силы находится согласно правилу левой руки или согласно определению векторного произведения. Модуль силы определяется

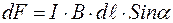, (2)

угол 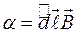между векторам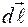и и .

Мы знаем, что ток создает магнитное поле, а также, что внешнее магнитное поле оказывает влияние на ток, поэтому интересно рассмотреть два параллельных прямых проводника, по которым текут ток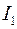и и 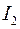. Каждый из токов создает свое магнитное поле, которое воздействует на другой ток. Сила такое действия – это сила Ампера.

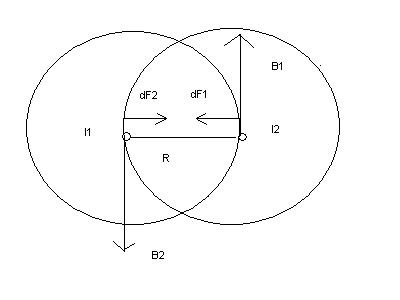
Пусть первый ток создает поле 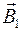. В этом поле на второй ток действует сила Ампера 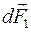. Т.к. угол между током 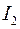и полем 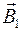прямой, то величина силы Ампера равна

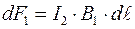
Величина магнитного поля, создаваемого прямым током 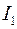равна 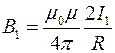, где 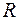- расстояние между токами (эту формулу получим в дальнейшем). Тогда сила, действующая на второй ток, определяется токами

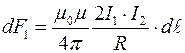
Аналогично можно найти выражение для силы, действующей на первый ток со стороны второго тока.

Замечаем, что силы по величине равны, но направлены в противоположные стороны.

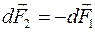
Величина силы взаимодействия двух токов .

Два одинаково направленных тока притягиваются друг к другу. Токи, напрвленные в противоположные стороны, отталкиваются.

СИЛА ЛОРЕНЦА

Т.к. ток - это направленное движение зарядов, то на движущийся заряд со стороны внешнего магнитного поля действует сила. Лоренц получил формулу для силы, которая действует на движущийся точечный заряд 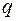со стороны магнитного поля .

(1)

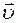- скорость заряда. Направление силы Лоренца для 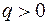определяется согласно правилу левой руки, либо согласно векторному произведению. Модуль силы Лоренца равен

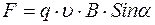
Для сила равна нулю. Когда угол равен 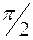, сила имеет величину 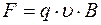. Т.о. сила Лоренца изменяет скорость только по направлению. Следовательно, магнитное поле не совершает работы над движущейся заряженной частицей. Когда, кроме магнитного поля, есть электрическое поле, полная сила Лоренца

имеет вид 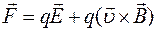. (2)

Рассмотрим движение точечной заряженной частицы в однородном магнитном поле. Пусть 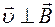. В этом случае величина силы Лоренца равна 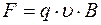. В этом случае частица всегда остается в плоскости, перпендикулярной магнитному полю. Поскольку по величине скорость не изменяется, то траекторией движения является окружность. Поскольку частица двигается по окружности на неё, кроме силы Лоренца действует центростремительная сила. Для любой точки траектории выполняется равенство сил.

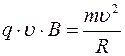. Отсюда находим радиус окружности 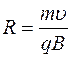. Период вращения . Для нерелятивистской частицы период не зависит от скорости. Поведение частицы в МП лежит в основе конструкции ускорителей. Для произвольной ориентации скорости частицы и направления магнитного поля, скорость можно разложить на параллельную и перпендикулярную компоненты: . В этом случае радиус окружности определяется 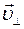: 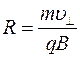. За период частица пройдет расстояние вдоль поля равное 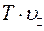. Если сложить эти два движения, то получим траекторию, которая является винтовой линией или спиралью с шагом

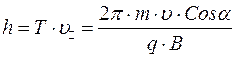
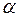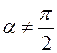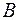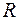где - угол между скоростью и магнитным полем. Пусть магнитное поле неоднородное, угол и поле растет в направлении , тогда и 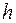уменьшаются с ростом 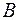. На этом эффекте основана фокусировка заряженных частиц в магнитном поле.

Эффект Холла

Мы познакомились с движением свободного заряда в МП. Выяснили, что на него со стороны МП действует сила Лоренца. Носителями тока в металлах и полупроводниках являются свободные электроны. В металле свободные электроны двигаются хаотично. Если к металлу приложить разность потенциалов, то электроны приобретут скорость, их движение станет упорядоченным, возникнет электрический ток. Поместим металлическую пластинку в магнитное поле, перпендикулярное приложенному электрическому полю. Тогда на движущиеся свободные электроны в металле со стороны магнитного поля будет действовать сила. Она направлена перпендикулярно току и магнитному полю. Под её действием электроны приобретут скорость в направлении силы. В итоге на одной из сторон пластинки будет избыток электронов. Они создают свое электрическое поле, действие которого компенсирует силу Лоренца. Установится стационарное состояние, соответствующее стационарному распределению заряда в поперечном направлении. Это эффект Холла.

На рисунке изображена металлическая пластинка с поперечными размерами: и 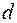. Разность потенциалов создает ток электронов, плотность которого 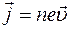. 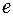- заряд электрона, 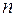- концентрация электронов в металле. Поскольку заряд электрона отрицательный, он двигается в сторону противоположную . Приложенное МП направлено перпендикулярно току. Сила Лоренца направлена вверх. В итоге на верхней грани имеем избыток электронов, на нижней – их недостаток. Возникающее в результате электрическое поле 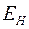уравновешивает силу Лоренца. 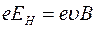. Напряженность 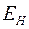можно выразить через разность потенциалов: . - холловская разность потенциалов. Сила тока 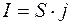, где - площадь поперечного сечения. Подставим выражение для плотности тока . Из этого выражения находим скорость . Найдем разность потенциалов . Заменяя скорость, получим

.

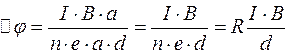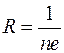- постоянная Холла. Таким образом, мы выразили неизвестную величину 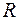через параметры, которые измеряются экспериментально. Эффект Холла используется для исследования природы проводимости и при изготовлении некоторого вида оборудования.

Циркуляция магнитного поля

Циркуляцией вектора по замкнутому контуру называется интеграл

Если контур охватывает источники магнитного поля, то этот интеграл отличен от нуля. В противном случае интеграл равен нулю. Сформулируем закон полного тока (теорема о циркуляции)

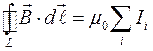(1)

В правой части стоит алгебраическая сумма всех токов, которые охватываются контуром. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Ток считается положительным, если его направление и направление обхода контура образуют правовинтовую систему. Ток противоположного направления считается отрицательным.

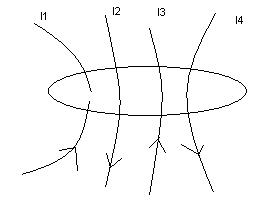
Закон (1) удобно использовать, когда система обладает высокой симметрией. Рассмотрим ток 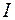, текущий по прямому бесконечному проводнику. Найдем магнитное поле этого тока.

Система обладает высокой симметрией: любую точку этого провода можно рассматривать как начало координат. Поворот пространства вокруг провода не изменяет физических характеристик системы. Поэтому контур интегрирования выбираем в виде окружности, плоскость которой перпендикулярна проводнику и её начало располагается на проводе. Точка наблюдения находится на окружности. Распишем интеграл (1)

Криволинейный интеграл равен:

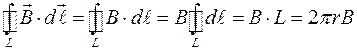. Приравнивая части закона полного тока, получим 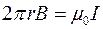. Находим величину поля 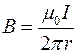. Этот результат мы использовали ранее. Если вычислить циркуляцию статического электрического поля, получим нуль, поскольку является потенциальным полем. Циркуляция магнитного поля не равна нулю. Такое поле называется вихревым.