Магнитное поле соленоида

Используя теорему о циркуляции, найдем МП соленоида (цилиндрической катушки) длиной 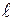. Для простоты расчета полагаем, что поле соленоида конечной длины совпадает с полем бесконечно длинного соленоида. Это позволит применить теорему о циркуляции, вследствие высокой симметрии задачи. Из эксперимента известно, что магнитное поле внутри такого соленоида однородное. Вне соленоида оно практически рано нулю. Конечно, такая замена вносит некоторую ошибку в определение МП из-за граничных эффектов. 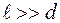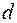Чем длиннее соленоид ( , где - диаметр катушки), тем меньше влияние граничных эффектов.

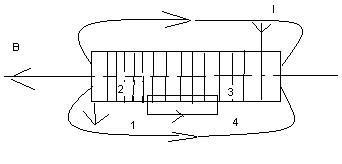
Выберем контур интегрирования (на рисунке 1234). Обход контура согласован с направлением тока в обмотках соленоида и направлением МП. Распишем контурный интеграл:

.

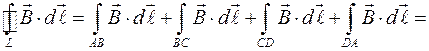
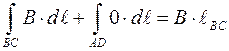На участках 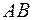и 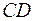вектор перпендикулярен вектору элемента контура 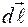. Участок 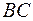расположен внутри контура, параллелен оси симметрии катушки и в силу однородности поле постоянное в любой точке этой прямой. Участок 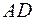находится вне соленоида, где МП равно нулю. Считаем, что длина прямой 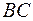равна длине соленоида 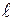. Согласно теореме полного тока, данный контур охватывает ток равный 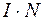, где 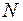- число витков катушки. Поставим значения интеграла и тока в Ур. (1).

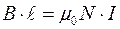или .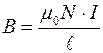

Это выражение определят величину МП в соленоиде. Краевыми эффектами пренебрегли.