Математическая модель нейрона и нейронных сетей
Математическая модель нейрона была создана на основе представления нейрона в виде элемента, суммирующего сигналы, поступающие в него через синаптические связи [2,3,4,16,18]. Каждому синапсу приписывается определенный коэффициент передачи (вес) электрических сигналов нервной системы. Нелинейные свойства нейрона моделируются с помощью специальной функции, которую часто называют “активационной”. Простейшая модель нейрона приведена на рис.12.1.
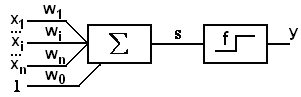
Рис.12.1. Модель нейрона
Вектор входного сигнала 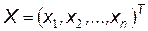 скалярно умножается на вектор весовых (синаптических) коэффициентов
скалярно умножается на вектор весовых (синаптических) коэффициентов 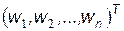 и к результату прибавляется смещение
и к результату прибавляется смещение 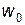 . Сигнал синаптической суммы
. Сигнал синаптической суммы 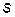 поступает на вход блока активационной функции
поступает на вход блока активационной функции 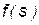 . Активационная функция исполняет роль ограничителя выходного сигнала, что присуще биологическим системам. Она определят вид нелинейности характеристик нейрона, расширяет его функциональные возможности. Математические зависимости модели нейрона имеют следующий вид:
. Активационная функция исполняет роль ограничителя выходного сигнала, что присуще биологическим системам. Она определят вид нелинейности характеристик нейрона, расширяет его функциональные возможности. Математические зависимости модели нейрона имеют следующий вид:
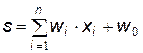 ,
, 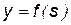 .
.
В качестве активационной функции используются либо ступенчатые функции, либо непрерывные функции. Первый тип функций проще реализуется, а второй необходим для аналитических исследований свойств нейронов. Одна из возможных форм задания непрерывной активационной функции (sigmoid function) и ее первой производной:
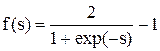 ,
, 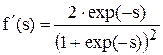 .
.
График активационной функции представлен на рис.12.2.
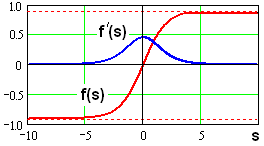
Рис.12.2. Непрерывная активационная функция
Известна [18] стохастическая модель нейрона, которая определяется с помощью ступенчатой активационной функции путем введения определенной вероятности активации нейрона (probability of firing) 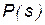 и имеет следующий вид:
и имеет следующий вид:
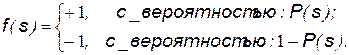
Множество связанных нейронов образуют нейронные сети (НС). НС в зависимости от вида основных элементов можно классифицировать следующим образом [10]:
1. По структуре сети: сети полносвязанные (fully connected), неполносвязанные (partially connected), сети слоистые, сети специальной структуры.
2. По типу взаимодействия нейронов: сети с парным взаимодействием, сети с множественным взаимодействием, сети с взаимодействием нейрона с самим собой, сети с симметричным и несимметричным взаимодействием.
3. Сети с дискретными и непрерывными состояниями нейронов.
4. Сети с дискретным и непрерывным временем.
5. Сети с детерминированной или стохастической динамикой, сети синхронного, параллельного или последовательного действия.
6. Сети с различными функциями возбуждения нейронов.
7. Сети с различными алгоритмами обучения и самообучения.
Нейронные сети могут обучаться, то есть изменение весовых коэффициентов по определенному правилу позволяет получить на выходе НС требуемые сигналы для определенных входных сигналов. Обучение представляет собой рекуррентную процедуру, в процессе которой образы обучающей выборки несколько раз подаются на вход НС. Порядок подачи может быть циклическим или случайным. Начальные значения должны быть ненулевыми, рекомендуется присваивать им случайные значения. Пример многослойной НС приведен на рис.12.3. НС состоит из k-слоев, имеет m-входных линий и n-выходных элементов.
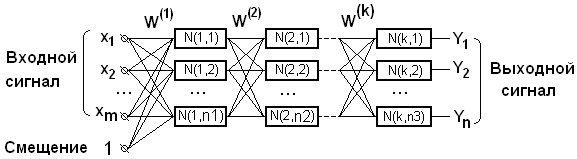
Рис.12.3. Многослойная полносвязанная НС.
Входные образы НС принято представлять в виде векторов. На вход НС можно подавать образы, соответствующие изображениям, звукам и наборам измерительной информации. Дискретные изображения структурно соответствуют матрицам, поэтому перед подачей на вход НС изображения векторизуют, то есть преобразуют в вектор путем последовательного перемещения столбиков один под другим в один общий столбик вектора. Единичный сигнал смещения можно считать последним элементом входного вектора 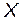 , а соответствующие весовые коэффициенты станут нижней строкой матрицы весовых коэффициентов
, а соответствующие весовые коэффициенты станут нижней строкой матрицы весовых коэффициентов 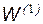 .
.
Математическая модель НС, приведенной на рис.12.3, основана на матрицах весовых коэффициентов и имеет следующий вид:
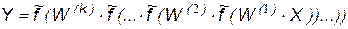 ,
,
где 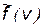 - оператор поэлементного вычисления активационной функции
- оператор поэлементного вычисления активационной функции 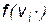 для элементов векторного аргумента
для элементов векторного аргумента 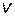 . Матрицы весовых коэффициентов объединяют нейроны слоя: каждой строке матрицы соответствует набор весовых коэффициентов соответствующего нейрона. Если НС является полносвязанной, то перестановка строк в матрицах внутренних слоев не изменит выходной вектор.
. Матрицы весовых коэффициентов объединяют нейроны слоя: каждой строке матрицы соответствует набор весовых коэффициентов соответствующего нейрона. Если НС является полносвязанной, то перестановка строк в матрицах внутренних слоев не изменит выходной вектор.
Нейронные сети являются универсальными аппроксиматорами [2], так как на них распространяется теорема Колмогорова-Арнольда: непрерывная функция нескольких переменных может быть представлена в виде суперпозиций и операций сложения функций одной переменной.
Дата добавления: 2016-02-16; просмотров: 1473;
