Движение тел в жидкостях

Сопротивление движению тел в жидкостях. Проведение ряда процессов химической технологии связано с движением твердых тел в капельных жидкостях или газах. К таким процессам относятся, например, осажде­ние твердых частиц из суспензий и пылей под действием сил тяжести и инерционных (например, центробежных) сил, механическое перемеши­вание в жидких средах и др. Как отмечалось, изучение закономерностей этих процессов составляет внешнюю задачу гидродинамики.

При движении тела в жидкости (или при обтекании неподвижного тела движущейся жидкостью) возникают сопротивления, для преодоления которых и обеспечения равномерного движения тела должна быть затра­чена определенная энергия. Возникающее сопротивление зависит главным образом от режима движения и формы обтекаемого тела,

При ламинарном движении, наблюдающемся при небольших скоростях и малых размерах тел или при высокой вязкости среды, тело окружено пограничным слоем жидкости и плавно обтекается потоком (рис. II-20, а). Потеря энергии в таких условиях связана в основном лишь с преодоле­нием сопротивления трения.

С развитием турбулентности потока (например, с увеличением скорости движения тела) все большую роль начинают играть силы инерции. Под действием этих сил пограничный слой отрывается от поверхности тела, что приводит к понижению давления за движущимся телом в непосред­ственной близости от него и к образованию беспорядочных местных зави­хрений в данном пространстве (рис. II-20, б). При этом разность давлений жидкости на переднюю (лобовую) поверхность тела, встречающую обте­кающий поток, и на его заднюю (кормовую) поверхность все больше превы­шает разность давлений, возникающую при ламинарном обтекании тела.

Начиная с некоторых значений критерия Рейнольдса, роль лобового сопротивления становится преобладающей, а сопротивлением трения можно практически пренебречь. В данном случае, как и при движении жидкости по трубам, наступает автомодельный (по отношению к критерию Рей­нольдса) режим.

Сила сопротивления R(н) среды движущемуся в ней телу может быть выражена уравнением закона сопротивления:

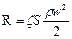(II,62)

где S — площадь проекции тела на плоскость, перпендикулярную направлению его дви­жения, м², w — скорость, м/сек, r — плотность среды, кг/м², x—коэффициент сопротивле­ния среды

Отношение R/S представляет собой перепад давлений Dр (н/м²), пре­одолеваемый движущимся телом. Поэтому, решив уравнение (II, 62) относительно x, можно установить, что коэффициент сопротивления x пропорционален критерию Эйлера 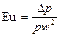(x отличается от Еu лишь множителем 2). Соответственно уравнения для расчета x при различных гидродинамических режимах могут быть получены обработкой опытных данных в виде обобщенных зависимостей между критериями гидродина­мического подобия.

На рис, II-22 представлена зависимость x от критерия Рейнольдса при движении шарообразных частиц диаметром d. Этот диаметр и является определяющим размером в критерии Re. Из графика видно, что сущест­вуют три различных режима движения, каждому из которых соответствует определенный характер зависимости x от Re:

ламинарный режим (область действия закона Стокса) при­близительно при Re < 2

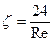(II,63)

переходный режим при Re = 2-500

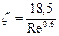(II,63a)

автомодельный режим (область действия квадратичного закона сопротивления Ньютона) при ~2·10⁵ > Re > -500

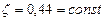(II,63б)

Подстановка в уравнение (II, 62) каждого из приведенных выше урав­нений для x показывает, что при ламинарном режиме сила сопротивления пропорциональна скорости в первой степени, т.е. R ~ w, при переход­ном режиме R ~ w^1,4, а при автомодельном режиме R » w².

При движении тел, отличающихся по форме от шара, значения коэф­фициента сопротивления больше и зависят не только от критерия Re, но и от фактора формы Ф, т.е.

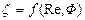(II,64)

Здесь

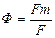(II,65)

где F_ш — поверхность шара, имеющего тот же объем, что и рассматривае­мое тело поверхностью F. Например, для куба Ф — 0.806; для цилиндра высотой, в 10 раз превышающей его радиус, Ф = 0.69; для диска, высота которого в 10 раз меньше радиуса, Ф = 0.32. Значения Ф приводятся в справочниках.

Надо заметить, что на самом деле роль фактора формы не всегда может быть сведена лишь к соотношению поверхностей. Поэтому наиболее надежные данные о численных зна­чениях Ф для тел различной формы получаются экспериментально.

Для тел нешарообразной формы определяющим линейным размером в критерии Re служит диаметр эквивалентного шара d, равный диаметру шара, имеющего такой же объем, что и данное тело. Если объем тела V, его масса т, а плотность r_т, то значение d может быть най­дено из соотношения

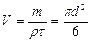
Осаждение частиц под действием силы тяжести. Рассмотрим движение тела в жидкости на примере осаждения твердой частицы в неподвижной среде под действием силы тяжести. Другой пример, связанный с анализом движения в жидкостях механических мешалок, приведен позже.

Если частица массой m (и весом mg) начинает падать под действием силы собственного веса, то скорость ее движения первоначально возрастает со временем. При полном отсутствии сопротивления среды скорость w менялась бы во времени по известному закону w = gt. Однако с увеличением скорости будет расти, согласно уравнению (II,62), сопротивление движению частицы и соответственно уменьшаться ее ускорение. В результате через короткий промежуток времени наступит равновесие: сила тяжести, под действием которой частица движется, станет равна силе деления среды. Начиная с этого момента, ускорение движения будет нулю; и частица станет двигаться равномерно — с постоянной скоростью. Скорость такого равномерного движения частицы в среде назы­вают скоростью осаждения и обозначают символом w_oс.

Сила, движущая шарообразную частицу диаметром d, выражается раз­ностью между ее весом и выталкивающей архимедовой силой, равной весу жидкости (среды) в объеме частицы:

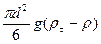
где r_т — плотность твердой частицы; r — плотность среды.

Сила сопротивления среды, в соответствии с уравнением (II,62)

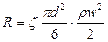
Скорость осаждения w_ос можно найти из условия равенства силы, дви­жущей частицу, и силы сопротивления среды:

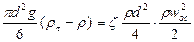
откуда

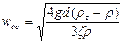(II,66)

Значение коэффициента сопротивления x может быть определено по одной из зависимостей — (II,63), (II,63а) или (II,63б). При подстановке в уравнение (II,65) выражения (II,63) для ламинарной области находим формулу

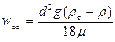(II,66а)

где m— вязкость среды.

Это же уравнение можно получить и при использовании выражения закона Стокса, согласно которому сопротивление среды при осаждении в ней мелких частиц выражается зависимостью

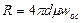(II,67)

Приравниваем действующую силу силе сопротивления середы

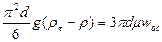
и, определив из этого выражения w_ос, получаем уравнение (II,67).

Максимальный размер частиц, осаждение которых происходит по закону Стокса, можно найти, подставив в уравнение (II,67) вместо скорости осаждения ее выражение через критерии Рейнольдса 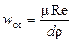и приняв Re = 2, т.е. — предельному значению Re для ламинарной об­ласти. Тогда

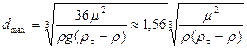(II,68)

Существует и минимальный размер частиц, ниже которого наблюдаются отклонения от закона Стокса. Нижний предел применимости закона Стокса соответствует Re » 10^-4. При Re £ 10^-4 на скорость осаждения очень мелких частиц начинает влиять тепловое движение молекул среды. В таких условиях размеры d частиц становятся соизмеримыми со средней длиной l свободного пробега молекул среды. При этом скорость осаждения оказывается ниже рассчитанной по уравнению (II,66). Поэтому вели­чину w_oc, определенную по уравнению (II,66а), следует разделить на поправочный коэффициент

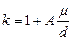(II,69)

причем величина А меняется в пределах от 1,4 до 20 (для воздуха А = 1.5).

Расчеты показывают, что при осаждении в воздухе частиц пыли раз­мером d > 3 мкм коэффициент k » 1. При d » 0.1 мкм пыль не осаж­дается, а наблюдается лишь хаотическое броуновское движение ее частиц.

В случае переходной области 2 < Re < 500 после подстановки в уравнение (II,68) выражения (II,62а) для l и некоторых преобразова­ний получим

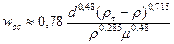(II,70a)

Аналогично для автомодельной области (при Re > 500), согласно вы­ражению (II,62б), подставив l = 0.44 в уравнение (II,65), находим

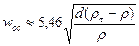(II,70б)

Для того чтобы выбрать расчетное уравнение, соответствующее данной области осаждения, т.е. одно из уравнений (II,70), (II,70а) или (II,70б), необходимо предварительно знать значение критерия Re, в который вхо­дит искомая скорость осаждения w_ос. Поэтому расчет w_оc по приведенным выше уравнениям возможен только методом последовательных прибли­жений. Допуская, что осаждение происходит в определенной области, например ламинарной, рассчитывают по соответствующему уравнению w_ос и по этому значению вычисляют Re. Затем проверяют, лежит ли най­денное значение Re в пределах, отвечающих принятой области осаждения. В случае несовпадения расчет повторяют до получения сходимых резуль­татов.

Вследствие трудоемкости метода последовательных приближений более удобно для определения w_oc пользоваться другим методом, предложен­ным П.В. Лященко. Этот метод основан на преобразовании уравнения (II,64) путем подстановки в него скорости осаждения, выраженной через Re, и возведения обеих частей уравнения в квадрат:

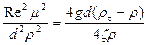
Отсюда

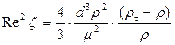(70)

Выражение в правой части этого уравнения принципиально не отли­чается от выражения (II,71) для критерия Аr:

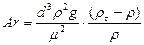(II,71a)

В данном случае за определяющий линейный размер принят диаметр частицы, а за масштаб разности плотностей частицы и среды — плотность среды, в которой происходит осаждение.

В критерий Архимеда искомая скорость осаждения не входит. Он состоит из величин, которые обычно либо заданы, либо могут быть зара­нее определены.

Таким образом

(II,72)

Подставив в это обобщенное уравнение критические (граничные) зна­чения критерия Re, отвечающие переходу одной области осаждения в дру­гую, можно найти соответствующие критические значения критерия Аr.

Для области действия закона Стокса (Re < 2) при подстановке выра­жения l, согласно зависимости (II,62), в уравнение (II,72) получим

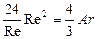
откуда

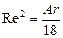(II,72a)

Верхнее предельное, или критическое, значение критерия Архимеда для этой области

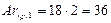
Следовательно, существование ламинарного режима осаждения соот­ветствует условию Ar £ 36.

Для переходной области, где 2 < Re < 500, подставляем значение x, согласно зависимости (II,62а), в уравнение (II,72). Тогда

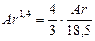
или

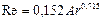(II,72б)

При подстановке в уравнение (II,72б) критического значения Re = 500 находят верхнее предельное значение Ar для переходной области

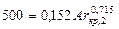
откуда

Аr_кр;2 = 83000

Таким образом, переходная область осаждения соответствует измене­нию критерия Ar в пределах 36 < Ar < 83 000.

Для автомодельной области, где Ar > 83 000, зависимость между Re и Ar можно найти, подставив l = 0.44, в соответствии с выражением (II,72б), в уравнение (II,72а):

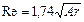(II,72в)

Таким образом, рассчитав критерий Ar, определяют по его значению область, в которой происходит осаждение. Вычисляют, пользуясь одним из уравнений (II,72а), (II,72б) или (II,72в), отвечающим этой области, значение Re и находят по нему скорость осаждения

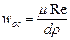(II,73)

Зная область осаждения, можно также рассчитать скорость осаждения по одному из уравнений (II,66), (II,66а) или (II,66б).

Для расчетов может быть использована и единая интерполяционная зависимость, связывающая критерии Re и Ar для всех режимов осаждения:

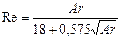(II,73а)

При малых значениях Ar вторым слагаемым в знаменателе можно пренебречь, и уравнение (II,73а) превращается в уравнение (II,120а), соответствующее области действия закона Стокса; при больших же зна­чениях Ar пренебречь можно уже первым слагаемым в знаменателе, и уравнение (II,73) превращается в уравнение (II,72в), отвечающее авто­модельной области.

Скорость осаждения w_ос частиц нешарообразной формы меньше, чем скорость осаждения шарообразных частиц. Чтобы ее рассчитать, значе­ние скорости осаждения w_ос для шарообразных частиц необходимо умно­жить на поправочный коэффициент j, называемый коэффициен­том формы

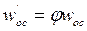(II,74)

Коэффициент j < 1, и его значения определяют опытным путем. Так, для Частиц округлой формы j » 0.77, для угловатых частиц j » 0.66, для продолговатых частиц j » 0.58 и для пластинчатых частиц j » 0.43.

Кроме того, при расчете скорости осаждения частиц нешарообразной формы в соответствующие уравнения для определения скорости следует подставлять указанный выше диаметр эквивалентного шара.

Приведенный расчет w_oc и w'_oc относится к скорости свободного осаждения, при котором осаждающиеся частицы практически не оказывают влияния на движение друг друга. При значительной концен­трации твердых частиц в среде происходит стесненное осажде­ние, скорость которого меньше, чем свободного, вследствие трения и соударений между частицами. Расчет w_ос при стесненном осаждении рас­смотрен позже, посвященной разделению неоднородных смесей.

В случае движения жидких капель в газе или в другой жидкости и пузырьков газа в жидкости уравнения для расчета w_ос усложняются даже для одиночных капель и пузырей вследствие изменения при движе­нии их формы.