Элементы гидродинамики двухфазных потоков

Многие процессы химической технологии проводятся при движении через трубопроводы и аппараты двухфазных потоков. В этих потоках одна из фаз обычно является дисперсной, а другая — сплошной (дисперсионная среда), причем первая распределена в объеме второй в виде частиц, капель, пузырей, пленок и т.п. Взаимное направле­ние обеих фаз в потоке может быть различным. Например, движение твердых частиц и потока газа при пневмотранспорте, пузырей пара и кипящей жидкости в вертикальных трубках выпарных аппаратов с есте­ственной циркуляцией направлено в одну сторону, т.е. является прямоточным. Во многих других случаях фазы движутся в противоположных направлениях, т.е. их движение противоточное. При противотоке фаз осуществляется, в частности, взаимодействие пленок стекающей вниз жидкости с восходящими потоками газа или пара в пленочных или насадочных абсорбционных и ректификационных колон­нах, взаимодействие капель с потоком другой жидкости (сплошной фазой) в полых или насадочных колонных экстракторах и т.д. Картина взаимного движения фаз в аппарате в целом или на отдельных его участках часто более сложная, чем при прямотоке или противотоке, напри­мер в аппаратах с псевдоожиженным слоем или на тарелках массообменных аппаратов при барботаже.

В двухфазных потоках, кроме границы раздела между сплошной фазой и стенками трубопровода или аппарата, имеется другая граница, раз­деляющая обе движущиеся фазы. В зависимости от вида этой границы раз­личают два рода двухфазных потоков:

потоки, в которых сплошной фазой является газ или жидкость, а дис­персной — твердая фаза;

потоки систем газ (пар)-жидкость и жидкость-жидкость (т.е. потоки двух несмешивающихся жидкостей).

Основное различие механизмов движения двухфазных потоков первого и второго рода состоит в том, что твердые частицы в таких процессах, как осаждение, псевдоожижение, пневмотранспорт, практически не меняют своей формы и массы, в то время как элементы дисперсных фаз в потоках систем газ-жидкость и жидкость-жидкость (пузыри, капли, пленки) обычно меняют при движении свою форму (из-за подвижности границы раздела фаз), а часто и массу (вследствие слияния или дробления отдель­ных пузырей и капель).

Гидродинамические характеристики двухфазных потоков первого рода были рассмотрены выше.

Математическое описание движения систем газ-жидкость и жид­кость-жидкость и получение уравнений для гидравлического расчета аппаратов, в которых они движутся, является значительно более слож­ным, чем для однофазных потоков. Поэтому приходится обычно исполь­зовать экспериментальный путь изучения двухфазных потоков, проводя опыты на моделях и обобщая результаты экспериментов. Одна из главных трудностей таких исследований связана с тем, что характеристики тече­ния каждой фазы во многих случаях зависят от условий течения другой фазы.

Для обобщения результатов опытов на двухфазных системах нередко применяют метод анализа размерностей. При этом появляется необходимость учитывать в числе переменных, от которых зависит протекание процесса, в частности, межфазное натяжение s. В результате получают помимо рассмотренных выше критериев гидродинами­ческого подобия еще один безразмерный комплекс, называемый критерием Вебера:

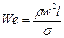(II,91б)

где l — характерный геометрический размер (например, диаметр капли).

Критерий We является мерой отношения сил инерции к силам межфазного натяжения и характеризует постоянство этого отношения в сходственных точках подобных потоков.

Кроме того, при описании поведения двухфазных систем часто оказывается необходи­мым использование дополнительных симплексов, характеризующих отношения свойств обеих фаз, например r₁/r₂, m₁/m₂ и др.

Гидравлические характеристики газо-жидкостных потоков в аппаратах различных типов, а также уравнения для гидравлического расчета этих аппаратов будут приведены в соответствующих главах. Здесь же в каче­стве примера кратко рассмотрим физическую картину и основные харак­теристики двух распространенных в промышленности процессов: барботажа газа (пара) сквозь жидкость и пленочного течения жидкости, сопри­касающейся с газом (паром).

Барботаж. При барботаже газа (пара) сквозь жидкость газовая фаза, распределяемая через отверстия различных устройств, диспергируется в последней в виде пузырей. Возникающую при этом дисперсию называют пеной. Такая пена является нестабильной и разрушается сразу же после прекращения подачи газа. Стабильные пены могут образовываться лишь при добавлении к жидкости поверхностно-активных веществ.

Пена может быть охарактеризована газосодержанием и удельной поверхностью контакта газа и жидкости.

Под газосодержанием (газонаполнением) пони­мают долю объема с газовой фазы в общем объеме пены. Эту величину можно определить с помощью измерения общего объема пены и объема «светлой» жидкости (последний измеряют после прекращения подачи газа).

Удельной поверхностью а (м²/м³) называют поверхность фазового контакта между газом и жидкостью в единице объема пены.

Зная эти характеристики, можно усреднить размер пузырей, находя­щихся в пене, и определить, средний поверхностно-объем­ный диаметр пузыря d_cp. Для его нахождения допустим, что в объеме V м³ содержится п пузырей. Тогда газосодержание e = пpd³_сp/6V, а удельная поверхность а = пpd³_сp/V. Определяя объем V из выражений для e и а и приравнивая оба значения V, получим

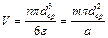
откуда после сокращения

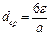(II,92)

Если газ распределяется в жидкости, проходя через одиночное отвер­стие, то при относительно небольшом расходе он барботирует сквозь жид­кость в виде отдельных свободно всплывающих пузырей (свободное движение).

Вычислим диаметр d пузыря в момент его отрыва. Обозначим через d₀ диаметр отверстия, r_ж и r_г — плотности жидкости и газа соответственно и s— поверхностное натяжение.

При свободном движении образующийся у отверстия пузырь сначала увеличивается в диаметре, а затем отрывается, когда подъемная (архимедова) сила, 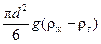, и сила сопротивления отрыву, зависящая от поверхностного натяжения (R = pd₀s), становятся равными друг другу. Отсюда выражение для расчета диаметра пузыря в момент отрыва:

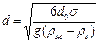(II,93)

Из уравнения (II, 93) следует, что при свободном движении диаметр пузыря не зависит от расхода газа, а определяется диаметром отверстия и физическими свойствами жидкости. С увеличением расхода газа Q (м³/сек) возрастает лишь число пузырей, отрывающихся в единицу времени, или частота отрыва, равная 6Q/pd³ сек^-1.

Когда расход газа достигает критического значения Q_кр, последова­тельно образующиеся у отверстия пузыри не успевают оторваться один от другого и движутся в виде цепочки, соприкасаясь друг с другом.

Значение Q_кр при этом равно:

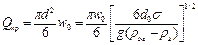(II,94)

где w_n — скорость подъема пузырей, м/сек.

При расходе газа выше критического диаметр пузырей увеличивается с возрастанием Q и составляет

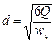(II,95)

Скорость подъема пузырей небольшого диаметра находится аналогично скорости свободного осаждения частиц — из условия равен­ства подъемной силы и силы сопротивления среды. Получаемое расчетное уравнение для w_п аналогично уравнению (II,86), в котором плотность r_т твердой частицы заменяется плотностью r_г газа, плотность r среды — плотностью r_ж жидкости, а знак перед правой частью уравнения меняется на обратный.

Режим движения пузырей определяется значением критерия Рейнольдса для пузыря

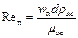
причем m_ж — вязкость жидкости.

Расчет диаметра пузырей (при условии, что они сохраняют при движении шарообраз­ную форму) можно производить по уравнениям: при ламинарном движении (Re_n < 9)

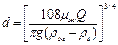(II,96)

при турбулентном движении (Re_n > 9)

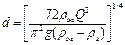(II,96a)

Уравнения (II,96) и (II.96а) пригодны лишь для пузырей диаметром не более 1−1.5 мм.

Закономерности движения пузырей большего диаметра будут отли­чаться от указанных выше закономерностей движения пузырей по сле­дующей причине. На пузырь газа (пара), всплывающий в жидкости, действуют три силы: подъемная (архимедова) сила, сила сопротивления окру­жающей жидкости и сила поверхностного натяжения. Благодаря действию силы поверхностного натяжения пузырь стремится сохранять шарообраз­ную форму, причем, чем меньше пузырь, тем больше сила поверхностного натяжения и тем устойчивее шарообразная форма пузыря. С увеличением размера пузыря из-за неравномерности давления по окружности пузырь все больше деформируется, отклоняясь по форме от шара. Для больших пузырей влияние поверхностного натяжения становится малым по сравне­нию с динамическим воздействием жидкой среды, и пузырь приобретает неустойчивую форму (рис. II-26): сначала эллипсоидальную (при d = 1−5 мм), а затем грибообразную (при d >5 мм). Изменение формы больших пузырей во времени при их всплывании приводит к колебаниям скорости движения пузы­рей и отклонениям направления их движения от вертикального. Движение таких пузырей иногда происходит по спиральным траекториям.

Картина массового барботажа в промышлен­ных аппаратах при истечении газа из многих отверстий значительно сложнее описанной выше. Это связано с тем, что пузыри всплывают не сво­бодно, а стесненно, воздействуя друг на друга, иногда сливаясь один с другим (явление коалесценции) или дробясь на более мел­кие пузыри и т.д. Анализ различных гидроди­намических режимов и расчетные зависимости для массового барботажа приведены в позже применительно к тарельчатым массообменным ап­паратам

Пленочное течение жидкостей. В ряде процессов химической техноло­гии (абсорбция, ректификация, выпаривание и др.) применяются аппараты, в которых жидкость движется по поверхности в виде тонких пленок. От характеристик течения пленок, их толщины и скорости движения в зна­чительной мере зависят скорости этих процессов.

Рассмотрим сначала стекание пленки жидкости под действием силы тяжести по вертикальной поверхности при условии, что газовый (паровой) поток не влияет на движение жидкости. Последнее условие соблюдается при небольших скоростях газа.

Гидродинамический режим движения пленки определяется критерием Рейнольдса для пленки:

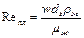
где w — средняя скорость движения пленки; d_э — эквивалентный диаметр пленки.

Эквивалентный диаметр пленки толщиной d определяется площадью сечения пленки S = Пd и периметром П поверхности, по которой дви­жется пленка:

(II,97)

(при движении пленки по внутренней поверхности трубы П = pd, где d—внутренний диаметр).

Подставив значение d_э в выражение для Rе_пл, получим

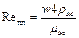
Из-за трудности измерения толщины и скорости движения пленки удобнее использовать в расчетах произведение wdr_ж, входящее в выраже­ние для Re_пл. Это произведение может быть записано в виде

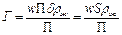(II,98)

Величину Г [кг/(м×сек)] называют линейной массовой плот­ностью орошения. Она представляет собой массу жидкости, про­ходящей в единицу времени через единицу длины периметра поверхности, по которой течет пленка. При подстановке Г = wdr8р_ж в выражение Re_пл получают следующее выражение критерия Рейнольдса для пленки:

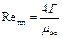(II,99)

Опытным путем установлено наличие трех основных режимов движе­ния пленки:

ламинарное течение пленки с гладкой (безволно­вой) поверхностью раздела с газом (Rе_пл < ~12);

ламинарное течение пленки с волнистой поверх­ностью раздела фаз (~12 < Re_пл < ~1600);

турбулентное течение пленки (Rе_пл > ~1600).

Для ламинарно-волнового течения, в свою очередь, различают два режима. При срав­нительно малых расходах жидкости, когда значение Rе_пл превышает 12, но не выше 100-200, под действием силы тяжести преимущественно образуются сравнительно «длинные» гравитационные волны. Длина их уменьшается с возрастанием скорости стеканий пленки. Вслед за этим первым ламинарно-волновым режимом (при больших значениях Rе_пл) наступает второй ламинарно-волновой режим. Для него характерно появление на поверхности плёнки «коротких» капиллярных волн или «ряби», возникающей под действием сил поверхностного натяжения (капиллярных сил). С дальнейшим увеличением расхода жидкости и Re_пл > ~1600 (критическое значение Rе_пл. по данным различных исследователей, составляет от 1000 до 2500) волнообразование на поверхности приобретает все более хаотический характер, причем по толщине пленки все сильнее развивается поперечное перемешивание, типичное для турбулентного режима. Переход от второго ламинарно-волнового режима к турбулентному режиму течения тонких пленок менее резок, чем при движении жидкости в трубах. Что касается чисто ламинарного (безволнового) течения пленок, то оно может быть достигнуто при значениях Rе_пл, харак­терных для ламинарно-волнового режима, лишь путем добавления к жидкости поверхно­стно-активных веществ.

При ламинарном течении пленки с гладкой поверхностью скорость по толщине ее изме­няется по параболическому закону от нуля у твердой стенки до w_mах у свободной поверх­ности, причем w_mах =1.5w, где w − средняя скорость пленки.

Расчет средней скорости w пленки и толщины d пленки при ламинарном течении произ­водят по теоретическим уравнениям:

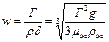(II,100)

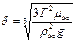(II,101)

Если поверхность не вертикальна, а наклонена под углом a к горизонту, то в эти уравне­ния вместо g вводят произведение gsina.

При турбулентном течении w и d можно рассчитывать по уравнениям, полученным обоб­щением опытных данных:

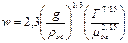(II,100a)

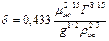(II,101a)

Для характеристики пленочного течения иногда используют понятие так называемой приведенной толщины пленки d_пр. Соотношение между действительной и приведенной толщинами пленки получается при замене в уравнении (II,101) величины Г на 1/4r_жRe_пл [в соответствии с уравнением (II,99)]:

(II,102)

где

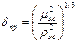(II,102a)

Течение пленки происходит под действием силы тяжести. Поэтому для его описания следует, помимо критерия Рейнольдса, применять либо критерий Фруда, либо производ­ный от него критерий Галилея:

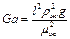(II,103)

где l — определяющий геометрический размер.

Очевидна связь между выражением для Ga и выражением для d_пр — приведенного линейного размера. Поэтому d_пр используют часто при описании пленочного течения вместо Ga. При этом d_пр имеет размерность длины, что и позволило формально назвать данную величину приведенной толщиной пленки.

При стекании пленки жидкости по внутренней поверхности верти­кальной трубы, по которой противотоком к жидкости, т.е. снизу вверх, движется поток газа (пара), скорость пленки и ее толщина не зависят от скорости газа до тех пор, пока эта скорость достаточно мала. В данном случае касательное напряжение в пленке максимально у твердой стенки и уменьшается до нуля на свободной поверхности. Однако с возрастанием скорости газа сила его трения о поверхность жидкости увеличивается. Как в газе, так и в жидкости у поверхности их раздела возникают равные, но противоположные по направлению касательные напряжения. При этом движение жидкой пленки начинает тормозиться, причем ее толщина увеличивается, средняя скорость снижается, а гидравлическое сопро­тивление аппарата газовому потоку возрастает. При определенной ско­рости газа (~5-10 м/сек) достигается равновесие между силой тяжести, под действием которой движется пленка, и силой трения у поверхности пленки, тормозящей ее движение. Это приводит к захлебыванию аппарата; наступление захлебывания сопровождается накоплением жидко­сти в аппарате, началом ее выброса и резким возрастанием гидравличе­ского сопротивления. Противоточное движение взаимодействующих фаз при скоростях выше точки захлебывания невозможно. Поэтому точка захлебывания соответствует верхнему пределу скорости для противоточных процессов в аппаратах любых типов.

При дальнейшем увеличении скорости газа в вертикальной трубе дви­жение пленки жидкости обращается, и она начинает «всползать» снизу вверх. Наступает режим восходящего прямотока газа и жидкости. Гидравлическое сопротивление при этом сначала снижается (по сравнению с сопротивлением, отвечающим точке захлебывания) до некоторого минимального значения, а затем снова возрастает. При увели­чении скорости газа выше 15-40 м/сек начинается брызгоунос, при котором жидкость отрывается от поверхности пленки и уносится газом в виде брызг.

В случае движения сверху вниз (нисходящий прямоток) газ увлекает пленку жидкости, увеличивая скорость пленки и уменьшая ее толщину. При одних и тех же скоростях газа гидравлическое сопро­тивление для нисходящего потока ниже, чем для восходящего. Устойчи­вый режим нисходящего прямотока существует при скоростях газа около 15-30 м/сек, выше которых происходит брызгоунос.

Описанные явления оказывают сильное влияние на скорость массопередачи и используются для интенсификации процессов в разрабатывае­мых в настоящее время аппаратах скоростного массообмена. В этой же главе приведены некоторые гидравлические характеристики широко распространенных в промышленности абсорбци­онных и ректификационных колонн с пленочным течением жидкостей,

Подробные сведения о характеристиках движения пузырей и капель и пленочного течения в различных условиях, в том числе при воздействии на них процессов тепло- и массообмена, содержатся в специальной лите­ратуре.