Пребывания жидкости в аппаратах

На многие процессы, главным образом тепловые, массообменные и хими­ческие, большое влияние оказывает структура потоков в аппаратах. Даже при первоначальном равномерном распределении входящих потоков (что само по себе часто представляет трудную задачу) картина их движе­ния внутри промышленного аппарата довольно сложна. Как правило, скорости потока неодинаковы по сечению аппарата, поперечному к основ­ному направлению движения, причем распределение, или профиль, ско­ростей изменяется от сечения к сечению по длине (высоте) аппарата. Частицы потока движутся по криволинейным, часто довольно сложным траекториям, иногда и в направлении, противоположном основному напра­влению потока. Это приводит к тому, что некоторые частицы могут быстро "проскочить" через аппарат, например в случае каналообразования и "байпасирования" части потока. Время пребывания этих частиц меньше среднего, в то время как другие задерживаются в аппарате дольше; зачастую в нем образуются застойные зоны, в которых время пребывания частиц оказывается весьма значительным.

Для полого аппарата (рис. II-27), например, время пребывания частиц, движущихся по траекториям, обозначенным стрелками 1, суще­ственно меньше времени пребывания частиц, которые циркулируют по стрелкам 2 или попадают в застойные зоны 3.

Другим примером, иллюстрирующим различие времен пребывания, может служить рассмотрение профиля скоростей при движении жидкости по трубе (см. рис. II-10). Различия в скоростях по сечению наи­более велики при ламинарном течении. Поэтому частицы, движущиеся вблизи оси трубы, обгоняют частицы, движущиеся ближе к ее стенкам, и находятся в трубе значительно меньшее время, чем последние.

При тур­булентном течении скорости распределены по сечению трубы более равно­мерно. Однако и в данном случае время пребывания разных частиц жид­кости неодинаково, что обусловлено турбулентными пульсациями, под действием которых происходит перемешивание частиц, или турбу­лентная диффузия: различные частицы движутся в разных направлениях по отношению к движению основной массы потока, в том числе и в поперечном (радиальная диффузия), и в продольном (осевая диффузия). Осевая диффузия может, как совпадать по напра­влению с движением основной массы потока, так и быть направлена в обратную сторону, в результате чего возникают различия во времени пребывания частиц жидкости. Радиальная же диффузия, выравнивая профиль скоростей, наоборот, сближает время пребывания разных частиц.

Во многих промышленных аппаратах картина распределения скоро­стей (поле скоростей) значительно сложнее, чем в приведенных выше отно­сительно простых примерах. Поле скоростей, в свою очередь, в значительной степени определяет профиль температур и концентраций от которых, как будет показано позже, зависит скорость тепловых и массообменных процессов и, в частности, их движущая сила. Те же факторы сильно влияют на скорость химических (реакционных) процессов.

Для частиц потока, наиболее быстро проходящих аппарат, время пре­бывания в нем недостаточно для достижения требуемой полноты протека­ния процесса. В то же время для частиц, попавших в застойные зоны, время пребывания слишком велико, и эти участки аппарата используются неэффективно, а иногда в них могут возникать также нежелательные процессы (например, побоч­ные реакции).

Игнорирование действительных полей скоро­стей, температур и концентраций и применение упрощенных представлений о структуре потоков обычно приводит к существенным ошибкам при расчете производственных аппаратов. Без учета структуры потоков в большинстве случаев невоз­можно использовать экспериментальные данные, полученные на установках лабораторного или полузаводского масштаба, для проектирования промышленной аппаратуры. Масштаб установки и даже небольшие изменения конструкции обычно сильно сказываются на структуре потоков. Это вызывает, как правило, снижение эффективности процесса в более крупных аппаратах по сравне­нию с ожидаемой на основании лабораторных опытов. Поэтому при масштабном пере­ходе от лабораторных установок к полузавод­ским и затем к промышленным целесообразно проводить гидравли­ческое моделирование. Оно заключается в изучении движе­ния потоков на "холодных" моделях, имеющих основные размеры моделируемых аппаратов, но изготовленных из более дешевых материалов. Как правило, эксперименты на таких моделях осуществляют не при рабочих, а при более низких температурах, и не с рабочими, а с более удобными для испытаний веществами (воздух, вода и т.п.). Наиболее точные данные о структуре потоков можно было бы получить путем непосредственного измерения скоростей во многих точках внутри аппарата или его модели. Однако выполнение таких измерений для аппа­ратов сложной конструкции представляет собой весьма трудную и Дорого­стоящую, а часто и практически неосуществимую задачу. Кроме того, даже в случае установления полной картины распределения потока в аппа­рате не всегда удается на практике использовать эти данные для расчета проводимого в аппарате процесса Вследствие того что старость является функцией всех координат, уравнения, характеризующие поле скоростей, сложны, и часто их решение в совокупности с уравнениями для ско­ростей тепло- и массопередачи и химических реакций невозможна или сильно затруднено.

По этим причинам более удобно, а зачастую практически единственно возможно, получать не непосредственную, а косвенную информацию о поле скоростей путем изучения распределения отдельных частиц жидко­сти по временам их пребывания в аппарате, т.е. выявлять, какая доля потока находится в аппарате то или иное время. Для этого, например, вводят в поток, поступающий в аппарат, примесь какого-либо вещества — индикатора и, анализируя во времени, содержание данного вещества в выходящей из аппарата «помеченной» жидкости, находят продолжи­тельность пребывания в аппарате отдельных ее частиц. В качестве инди­каторов применяют различные краски, растворы солей, изменяющих элек­тропроводность жидкости, радиоактивные препараты и другие вещества, концентрацию которых легко измерить. Отклик на возмущение, внесенное при этом на входе в аппарат вводом индикатора, представляют в. виде кривых зависимости концентрации его в выходящей жидкости от вре­мени, которые называют выходными кривыми, или кри­выми отклика (см. ниже).

При таком методе исследования механизм явлений, происходящих внутри аппарата, вскрыть труднее, так как само поле скоростей остается неизвестным. Однако достоинства указанного метода часто компенсируют этот его недостаток.

Данные о распределении времени пребывания получить проще, чем выявить полную картину распределения скоростей. Для этого достаточно провести соответствующие измерения лишь на входе и выходе потока. Кроме того, легче оказывается количественная трактовка получаемых результатов для расчета технологического процесса и управления им, так как здесь приходится иметь дело с функцией уже не нескольких, а единственной переменной — времени. При этом знания распределения времени пребывания частиц жидкости во многих случаях вполне доста­точно для расчетных целей. Наконец, данные о распределении времени пребывания нередко позволяют приближенно судить и о самом механизме движения потока, т.е. о его структуре внутри аппарата.

Пометим, например, порцию поступающей в какой-то момент в аппа­рат жидкости путем мгновенного ввода во входящий поток по всему его поперечному сечению какой-либо краски (импульсный ввод). Через неко­торый промежуток времени, анализируя содержание краски в потоке на выходе, мы обнаружим, что вся краска так же мгновенно; выйдет из аппа­рата. Этот результат однозначно будет свидетельствовать о такой струк­туре потока внутри аппарата, при которой все частицы жидкости движутся параллельно друг другу с одинаковыми скоростями, не обгоняя основную массу потока и не отставая от нее. Поток движется как бы аналогично твердому поршню и поэтому называется поршневым. Аппараты с поршневым движением жидкости называют аппаратами идеаль­ного вытеснения.

Времена пребывания т всех частиц потока в аппарате идеального вытес­нения одинаковы и равны среднему времени пребывания t_в (сек), которое определяется частным от деления длины l их пути на линейную скорость w жидкости, или

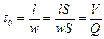(II,104)

где S — площадь поперечного сечения аппарата, м²; V — объем аппарата (для двухфаз­ного потока — объем, занимаемый потоком рассматриваемой фазы), м³; Q — объемный рас­ход жидкости (фазы), м³/сек.

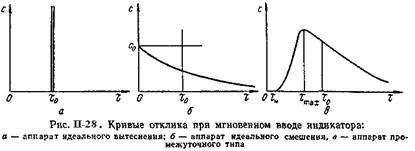
Вид кривой отклика при идеальном вытеснении представлен на рис. II-36, а. Начиная с момента t = 0, когда индикатор был введен во входящий поток, и до момента t = t₀, индикатор не обнаруживается в выходящем из аппарата потоке. В момент же времени t = t₀ концентрация с индикатора на выходе мгновенно возрастает (теоретически — до беско­нечности), а затем сразу же вновь снижается до нуля. Индикатор про­ходит через аппарат неразмываемым тончайшим слоем (как бы поверхностью твердого поршня), и сигнал, фиксируемый на выходе в момент t₀, в точности соответствует сигналу на входе в момент t = 0.

Идеальное вытеснение жидкости в чистом виде никогда не реализуется на практике. Поэтому аппарат идеального вытеснения является идеа­лизированной моделью. Однако в ряде случаев поток в реальных аппаратах более или менее приближается к поршневому. Сравни­тельно близки к аппарату идеального вытеснения, например, аппараты, в которых жидкость (газ) движется по длинным трубкам, заполненным зернистыми материалами (катализатором, адсорбентом).

В большинстве случаев структура потоков в аппаратах более или менее значительно отличается от структуры, отвечающей идеальному вытесне­нию. Это может быть следствием различных причин, в том числе — пере­мешивания частиц жидкости вдоль оси аппарата, различия скоростей по поперечному сечению ламинарного потока, байпасирования части потока вследствие каналообразования, образования застойных зон и т.д.

Перемешивание вдоль оси аппарата при этом, в свою очередь, может вызываться самыми разнообразными причинами. Оно может происходить под действием механической мешалки или вследствие естественной конвекции, обусловленной разностью плотностей жидкости в различных точках (например, в выпарных аппаратах с естественной циркуляцией, опи­санных в главе IX). Оно может быть также обусловлено турбулентной диффузией или увле­чением частиц потока одной из фаз потоком другой фазы при их противоточном взаимодей­ствии (например, при захвате некоторой доли движущейся вниз жидкости поднимающимися пузырями газа при барботаже) и другими причинами.

Однако какой бы ни была причина отклонений от идеального вытесне­ния, они проявляются в том, что времена пребывания т различных частиц уже неодинаковы и отличаются от среднего времени пребывания t₀ опре­деляемого по уравнению (II,104). Одни частицы обгоняют основную массу потока и появляются на выходе из аппарата раньше ее, другие задержи­ваются в аппарате.

Независимо от механизма любое отклонение от идеального вытеснения часто условно называют перемешиванием, или обратным перемешиванием. В этом смысле противоположной аппарату идеального вытеснения идеализированной моделью непрерывно действую­щих аппаратов считают аппарат идеального перемешива­ния, или идеального смешения.

Если в какую-то порцию непрерывно входящего в такой аппарат потока ввести определенное количество М₀ краски, то она мгновенно равномерно окрасит всю жидкость (или фазу — при двухфазном потоке) содержа­щуюся в аппарате. Концентрация (с₀) индикатора в любой точке аппарата в этот момент будет равна

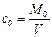(II,105)

После этого концентрация с краски в аппарате начнет убывать во вре­мени, так как краска непрерывно выносится потоком, а входящая жид­кость краски уже не содержит. Однако в любой момент концентрация краски остается одинаковой во всех точках аппарата.

Из соответствующей кривой отклика (рис. II-28,б) видно, что большая часть индикатора выходит в этом случае из аппарата за время между моментом его ввода (t = 0) и моментом, соответствующим среднему вре­мени пребывания t_в, определяемому по уравнению (II,104). Для вымыва­ния остальной части индикатора теоретически требуется бесконечное время.

Для описания закона изменения величины с во времени составим урав­нение материального баланса по индикатору. Пусть за произвольный про­межуток времени dt из аппарата выходит (вымывается) количество инди­катора dM. Это приводит к изменению (−dc) концентрации индикатора в объеме V, причем минус указывает на убывание концентрации. Тогда

dM = -Vdc = cQdt

где Q — объемный расход потока через аппарат, м³/сек. Отсюда с учетом выражения (II,104)

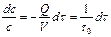
Это уравнение может быть проинтегрировано в пределах от с₀ (при t = 0) до с (в произвольный момент времени t):

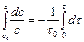
В результате интегрирования получим зависимость

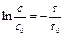
или

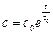(II,106)

Концентрацию индикатора и время можно выразить в виде относи­тельных (безразмерных) величин, приняв за масштаб концентрации зна­чение с₀, определяемое уравнением (II,104), за масштаб времени — сред­нее время пребывания t₀, определяемое уравнением (II,93), Обозначив С = c/c₀ и q = t/t₀, получим

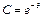(II,106a)

Примером аппарата, условия в котором близки к идеальному смеше­нию, является сосуд с интенсивно работающей мешалкой, через который непрерывно движется маловязкая жидкость при небольшом ее расходе. Близко к идеальному смешению и движение твердой фазы в кипящем слое зернистого материала при однородном псевдоожижении.

Картина движения потоков в большинстве непрерывно действующих аппаратов не отвечает ни идеальному вытеснению, ни идеальному смеше­нию. По структуре потоков эти аппараты можно считать аппаратами про­межуточного типа. Примерный вид кривой отклика для таких аппаратов представлен на рис. II-36, в. Введенный мгновенно (импульсом) во входящий поток индикатор появляется на выходе позднее, чем при идеальном смешении — через некоторое время t_н после момента ввода t = 0, Его концентрация на выходе сначала увеличивается во времени до момента t_max и лишь затем начинает уменьшаться, стремясь к нулю при t ® ¥. Кривая отклика на рис. II-28,в тем ближе по форме к кривым на рис. II-28,а или II-28,б, чем ближе движение потока в аппарате к условиям идеального вытеснения или идеального смешения соответ­ственно,

Для математического описания распределения времени пребывания жидкости в общем случае снова составим уравнение материального баланса по индикатору. Пусть за бесконечно малый промежуток dt между произвольным моментом времени t и (t + dt) из аппарата выйдет коли­чество индикатора dM. Если концентрация индикатора в выходящем потоке равна с, то за время dt поток уносит из аппарата с Qdt индикатора. Следовательно

dM = cQdt

Для определения всего количества М₀ индикатора, введенного в аппа­рат и полностью удаляемого из него за время t ® ¥, проинтегрируем это выражение в соответствующих пределах:

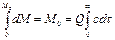(II,107)

Переходя к безразмерным концентрации С = с/с₀, времени q = t/t₀ и подставляя в уравнение (II,107) с = Сс₀ и t = qt₀, получим

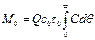
Подставляя М₀ =с₀V, согласно зависимости (II,104), и Q = V/t₀, в соответствии с выражением (II,105), имеем

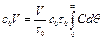
откуда

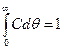(II,108)

Кривые отклика чаще всего строят не в координатах с − t (рис. II-29), а в безразмерных координатах С − q. При этом площадь под кривой отклика (рис. II-29) выражает, в соответствии с уравнением (II,108), общее относительное количество индикатора (или всей «помеченной» жидкости), принимаемое за единицу. В то же время величина Cdq (заштрихо­ванная накрест площадка на рис. II-29) характеризует долю общего количества индикатора, удаляемую из аппарата за время dq, или долю жидкости, пребыва­ние которой в аппарате соответ­ствует промежутку времени от q до (q + dq).

Зависимость концентрации С от времени q называется диф­ференциальной функ­цией распределения времени пребывания жидкости в аппарате Частный вид этой функции для аппарата идеаль­ного смешения выражен уравнением (II,106а).

Зависимость от q величины 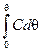, характеризующей долю индикатора, вышедшего из аппарата за время от 0 до произвольного момента q, назы­вают интегральной функцией распределения. В частности, заштрихованная параллельными линиями площадь на рис. II-37 характеризует долю индикатора, вышедшего из аппарата к моменту времени, равному среднему времени пребывания t₀, т.е. долю жидкости, время пребывания которой в аппарате не больше t₀.

Функция распределения времени пребывания потока в аппарате является типичной функцией распределения случайной величины. Для нахождения среднего значения времени пребывания, как и для любой случайной величины, используется зависимость

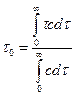(II,109)

Вместе с тем, согласно выражению (II,104), среднее время пребывания t₀ = V/Q, откуда

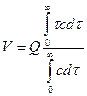(II,109a)

Уравнение (II, 109а) применяют для определения объема V, занимаемого в двухфаз­ном потоке внутри аппарата одной из фаз, расход которой составляет Q, например общего объема капель (дисперсной фазы) и сплошной фазы для системы жидкость — жидкость в экстракционных аппаратах и т.п.

Пользуясь данными о распределении времени пребывания, можно решать и другие прикладные задачи. Так, с помощью уравнений (II, 109а) или (II,107) можно найти расход жидкости через трубопровод, если обычные методы, описанные выше, нельзя применить.

При проведении химических, массообменных или тепловых процессов в аппаратах идеального вытеснения концентрации рабочих веществ (или температуры) непрерывно меняются от входа к выходу по длине (высоте) аппарата. В аппаратах идеального смешения происходит полное выравни­вание концентраций (или температур) по всему аппарату, причем в любой точке они равны значениям соответствующих величин на выходе потока.

Для обоих этих случаев методы расчета скоростей процессов и размеров соответствующих аппаратов при известных кинетических коэффициентах хорошо разработаны. Они будут подробно описаны в последующих главах. Значительно труднее описать и учесть реальное поле концентраций или температур при расчете аппаратов промежуточного типа.

Для описания действительной картины изменения концентраций (или температур) в этих аппаратах необходимо иметь какую-то количественную меру степени перемешивания, т.е. степени отклонения реальной гидро­динамической структуры потока от структуры, отвечающей идеальному вытеснению или идеальному смешению. Чтобы найти такую меру, выра­женную численными значениями какого-либо одного или нескольких пара­метров, обычно прибегают к описанию структуры потока при помощи той или иной упрощенной модели, или физической схемы, более или менее точно отражающей действительную физическую картину движения потока. Этой идеализированной физической модели отвечает математическая модель — уравнение или система уравнений, посредством которых расче­том определяется вид функции распределения времени пребывания. Далее сопоставляют реально полученный опытным путем (из кривых отклика) вид функции распределения с результатом расчета на основании выбран­ной идеальной модели при различных значениях ее параметра (или пара­метров). В результате сравнения устанавливают, соответствует ли с доста­точной степенью точности выбранная модель реальной гидродинамической структуре потока в аппарате данного типа, т.е. адекватна ли модель объекту. Затем находят те численные значения параметров модели, при которых совпадение опытной и расчетной функций распределения наи­лучшее. Указанные значения в дальнейшем применяют при расчете про­цесса в конкретном аппарате. Обобщая эти данные, получают уравнения для расчета значений параметров модели при разных гидродинамических условиях работы и размерах аппаратов данного типа.

В настоящее время для описания структуры потоков в аппаратах про­межуточного типа наиболее широко используют ячеечную и диффузион­ную модели.

В соответствии с ячеечной моделью аппарат рассматривается как бы состоящим из ряда последовательно соединенных по ходу потока одинаковых ячеек, или каскада ячеек, в каждой из которых поток идеально перемешан.

Наиболее близко этой модели от­вечает поток в реальном каскаде аппа­ратов с мешалками (рис. II-30, а). Применение ячеечной модели дает хоро­шие результаты также для массообменных аппаратов ступенчатого типа, например для тарельчатых колонн, описанных в последующих главах, и для других аппаратов, секционированных по ходу потока.

Единственным параметром ячеечной модели является число п таких ячеек, на которые нужно мысленно разбить аппарат, чтобы полу­чить реально достигаемую в нем сте­пень перемешивания потока. Если число ячеек оказывается близким еди­нице, то движение потока в аппарате приближается к идеальному смеше­нию.

Функция распределения времени пребывания для ячеечной модели в частном случае п = 1 описывается уравнением (II,106 а). Используя ме­тод, аналогичный примененному при выводе этого уравнения, для любого значения п находят функцию распределения общего вида

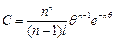(II,110)

Вид кривых отклика, соответствующих этой функции распределения при различных значениях п, показан на рис. II-30, б. С увеличением числа ячеек структура потока в аппарате все более отклоняется от идеального смешения и приближается к идеальному вытеснению. Идеальное вытесне­ние достигается при п ® ¥. Таким образом, аппарат идеального вытесне­ния можно представить как бесконечную последовательность ячеек иде­ального смешения.

В основу диффузионной модели положено допущение о том, что для математического описания процесса перемешивания потока может быть использовано уравнение, аналогичное уравнению диффузии в дви­жущейся гомогенной среде. Значит, эта модель исходят из приближенной аналогии между перемешиванием и диффузией. Согласно диффузионной модели, всякое отклонение распределения времени пребывания частиц потока от распределения при идеальном вытеснении, независимо от при­чины, вызвавшей это отклонение, считают следствием продольного перемешивания (вдоль оси потока), условно описываемого уравнением диф­фузии с некоторым фиктивным коэффициентом диффузии.

В соответствии с принятой аналогией, если в движущемся (например, по трубе) потоке окрасить тонкий поперечный слой жидкости; то краска будет размываться в обе стороны от движущегося окрашенного сечения. Как и в случае обычной молекулярной диффузии, размывание краски в этих направлениях обусловлено наличием градиента ее концентрации. Однако скорость такого размывания больше, чем в случае молекулярной диффузии. Поэтому для количественной характеристики скорости про­дольного перемешивания вместо коэффициента диффузии D, используе­мого в известных законах Фика, вводят некоторый фиктивный коэффициент диффузии Е, называемый также коэффи­циентом продольного перемешивания.

Диффузия в движущемся потоке описывается уравнением (X,19), подробно рассматриваемым в главе X. Записывая это уравнение в прило­жении к рассматриваемому случаю однонаправленной диффузии инди­катора (лишь вдоль оси х потока) и заменяя в нем коэффициент молеку­лярной диффузии D коэффициентом продольного перемешивания Е, получим

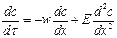(II,111)

Решение уравнения (II,111) для случая мгновенного ввода индикатора во входящий в аппарат поток приводит к следующему выражению функ­ции распределения времени пребывания:

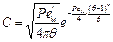(II,112)

Здесь Ре'_м — безразмерный комплекс величин, выражаемый соотно­шением

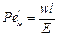(II,113)

где l — длина или высота аппарата.

Этот комплекс называют критерием Пекле для про­дольного перемешивания.

Такое название комплекс wl/E получил потому, что его выражение аналогично диф­фузионному критерию Пекле Ре' = wl/D, применяемому при расчете процессов массопередачи, в котором величина D заменена на Е. Нередко во избежание путаницы комплекс wl/E называют также критерием Боденштейна и обозначают сим­волом Во.

Критерий Ре'_м является единственным параметром диффу­зионной модели. По его численному значению можно судить о структуре потока, определяя количественно ее отклонения от идеального вытеснения, при котором Ре'_м → ¥, или от идеального смешения, кото­рому отвечает Ре'_м = 0. Построив, пользуясь уравнением (II,10), диффе­ренциальные функции распределения при различных значениях Ре'_м, можно убедиться, что вид соответствующих кривых меняется с изменением Ре'_м приблизительно так же, как при изменении п в случае применения ячеечной модели (рис, II-30, б).

Значение Ре'_м, как и п для ячеечной модели, зависит от конструкции и размеров аппарата и от гидродинамических условий в нем. Оно опреде­ляется также путем сопоставления опытных кривых отклика с рассчитан­ными по уравнению (II,112) для различных значений Ре'_м.

Диффузионную модель используют преимущественно для описания структуры потоков в аппаратах, не разделенных на ступени, например в массообменных аппаратах с непрерывным контактом фаз.

Когда значения Ре'_м или п достаточно велики (равны или больше десяти), расчеты на основе диффузионной и ячеечной моделей обычно дают близкие результаты; поэтому в таких условиях оказывается безраз­личным, какую из этих моделей применять.

Ячеечная и диффузионная модели, хотя и широко используются на практике, но не могут точно описать структуры потоков во всех реальных аппаратах. Поэтому кроме них разработаны другие модели; некоторые из них характеризуются не одним, а большим числом параметров. Такова, например, двухпараметрическая диффузионная модель, параметрами которой являются коэффициенты перемешивания в осевом и радиальном направлениях.

ЛЕКЦИЯ 4