Физические свойства жидкости основные методы их определения

Физические свойства жидкостей играют большую роль в металлургических процессах. Рассмотрим некоторые важнейшие физические свойства жидкостей,

Межфазное (поверхностное) натяжение.

Исторически сложилась такая ситуация, что понятие поверхностное натяжение можно ввести двумя различными, но эквивалентными путями.

Первый подход, изложенный в труде Лапласа "Небесная механика", рассматривает поверхностное натяжение как силу, действующую на единицу длинны контура поверхности жидкости, т.е. исходит из понятия напряжения теории упругости:

Определение. Поверхностным натяжением называют величину, численно равную половине силы, которую необходимо приложить к тонкой пластинке единичной длинны, чтобы оторвать ее от поверхности жидкости.

Такое определение конструктивно, т.е. при помощи него можно предложить метод измерения величины поверхностного натяжения σ. В ряде книг поверхностное натяжение обозначают другими символами - γ, T. Идеи методов измерения, непосредственно основанные на этом определении, принадлежат Вильгельми. Их принципиальная схема изображена на рисунке 2.8.

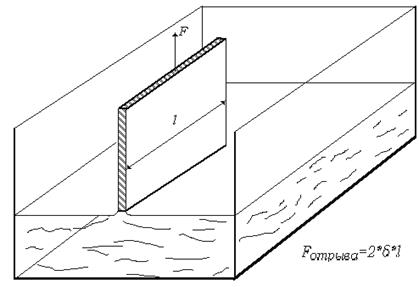
Рисунок 2.8. Схема эксперимента с пластинкой Вильгельми.

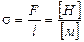Единицы измерения поверхностного натяжения в соответствии с определением σ равны:

Такой механический подход был скорее удобен для разработки методов измерения и не мог привести к включению поверхностных явлений в общую проблематику термодинамики.

Второй, энергетический подход разработан в рудах Гиббса.

Суть этого подхода заключается в следующем. На реальной границе раздела двух фаз, если ее рассматривать на микроуровне, происходит более или менее плавное изменение свойств, обусловленное дальнодействием межмолекулярных сил. На рисунке 2.9. изображено реальноеповедение плотности на поверхности раздела и идеальное представление. Гиббс показал, что идеальная граница раздела обладает избыточной энергией. При таком подходе поверхностное натяжение определяется так:

Определение.Поверхностным натяжением называют энергию, необходимую для увеличения площади поверхности раздела фаз на единицу

В соответствии с этим определением:

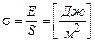
Анализ размерности показывает, что два определения совпадают:

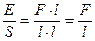
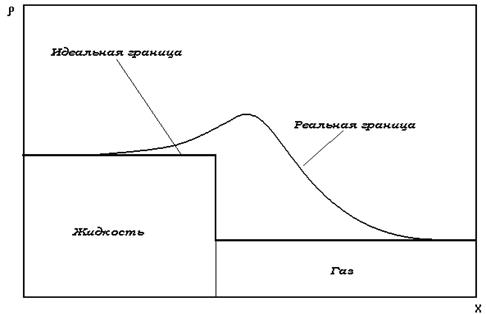Рисунок 2.9. Схема реальной и идеальной границы.

Второй подход позволяет утверждать, что для жидкостей с сильными связями поверхностное натяжение больше, чем для жидкостей со слабыми связями. Сравнение для жидкостей с различными типом связи дано в (Ванюков, Зайцев, 1973, с.154).

Таблица 2.1.

Поверхностное натяжение некоторых жидкостей

Металл Т, К s, мДж/м2 Металл Т, К s, мДж/м2

Na 371 191 Sn 523 540

Cu 1373 1350 Ag 1273 920

Au 1373 1125 Mg 973 560

Zn 673 760 Hg 298 470

Al 973 860 Ga 303 730

Ti 1945 1500 Zr 2128 1420

Si 1693 730 Pb 603 450

Nb 2733 1900 Sb 903 380

Bi 573 380 Fe 1823 1860

Co 1823 1870 Ni 1773 1750

Методы измерения поверхностного натяжения

Рассмотрим два наиболее популярных в пирометаллургии метода измерения поверхностного натяжения.

Метод лежащей капли разработан в середине прошлого века Башфортом и Адамсом. Суть метода заключается в измерении формы поверхности капли жидкости: лежащей на твердой поверхности - подложке. Принципиальная схема аппаратуры для измерения представлена на рисунке 2.10.

Рисунок 2.10. Схема измерения поверхностного натяжения методом лежащей капли.

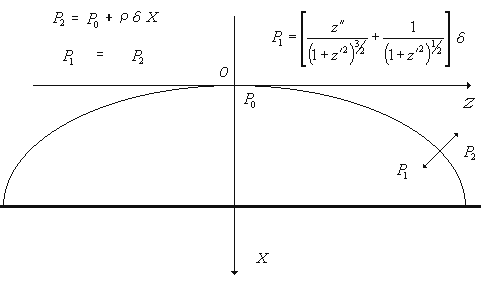
Рисунок 2.11. Форма лежащей капли.

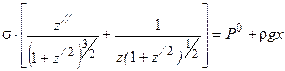Еще в 1806 году Пьер Лаплас в приложении к "Небесной механике" вывел формулу, определяющую форму поверхности лежащей капли, рисунок 2.11. Эта формула представляет собой нелинейное дифференциальное уравнение второго порядка:

Это уравнение неоднократно пытались решить аналитически. Такие попытки предпринимали Гаусс, Пуассон и многие другие. Однако численного решения найти не удалось*. В 1856 году Башфорт совместно с Адамсом (сыном астронома, открывшего планеты Плутон) впервые разрабатывают метод численного интегрирования дифференциальных уравнений. После этого Башфорт в одиночку в течение 28 лет, применяя численные методы, рассчитывает формы капель и составляет таблицы. Точность расчетов составляла 6 значащих цифр. После издания этих таблиц появилась реальная возможность определять поверхностное натяжение по форме лежащей капли. Для этого требуется зарисовать или сфотографировать мериадианальноесечение капли и, обмерив ее, составить таблицу зависимости z от x. В таблицах Башфорта необходимо найти ту таблицу, в которой рассчитанная форма в наибольшей степени совпадает с экспериментально определенной.

В настоящее время в ряде крупных металлургических лабораторий мира разработано специальное оборудование, позволяющее полностью автоматически произвести измерение поверхностного натяжение методом Башфорта. Лежащая капля проецируется на специальный экран, откуда данные поступают в компьютер. Компьютерная программа численно решает уравнение с разными значениями σ до тех пор, пока не найдет оптимальное.

Отметим, что и в XX веке продолжались попытки аналитически решить данное уравнение. Невозможность его аналитического решения до сих пор не доказана.

В 30-50-х годах, когда компьютеры еще не стали привычным инструментом металлурга-исследователя был разработан ряд упрощенных методов обмера формы капли. Наиболее известный из этих методов принадлежит Дорсею. По методу Дорсея требуется измерить лишь несколько величин, характеризующих форму капли, рисунок 2.12.

Рисунок 2.12. Величины, измеряемые по методике Дорсея.

После этого по формуле

можно рассчитать поверхностное натяжение. Формула была выведена Дорсеем по таблицам Башфорта.

Использование метода Башфорта для расплавов и непрозрачных жидкостей привело к созданию специальной экспериментальной техники, основанной на просвечивании капли рентгеновскими лучами. Таким методом были определены поверхностные натяжения для многих шлаковых систем и межфазное натяжение на границе штейн-шлак.

Метод максимального давления в пузырьке разработан Кантором. Сущность метода заключается в измерении давления, которое требуется для отрыва пузырька газа от поверхности тонкой трубки, помещенной в жидкость. Принципиальная схема установки этого метода представлена на рисунке 2.13.

Представим, что пузырек отрывающегося газа имеет форму полушара. Тогда отрыв пузырька произойдет после того, как работа по расширению газа в пузырьке сравняется с работой, затрачиваемой на образование новой поверхности жидкость-газ:

А_{РАСШИРЕНИЯ} = А_{ПОВЕРХНОСТИ}=P.V_ПУЗ = σ.S_ПУЗ=P.4/6.π.r³ = σ.2.π.r²

Отсюда следует, что измерив давление Р и зная внутренний радиус трубки, можно рассчитать поверхностное натяжение жидкости:

σ = 1/3.P.r

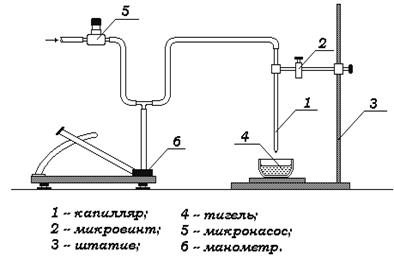
Рисунок 2.13. Схема установки для измерений по методу Кантора.

Полученная формула, разумеется, является упрощенной, т.к. мы предположили, что форма пузырька - полушар.

Плотность жидкости.

Плотность (или обратная ей величина молярный объем) играет важную роль в пирометаллургических процессах. Она влияет на процессы разделения расплавов в процессах плавки, гидравлику металлургических аппаратов, условия и характеристики процессов продувки жидких расплавов газом и т.д.

Определение плотности одно из самых простых из всех физических свойств:

Определение. Под плотностью понимают массу единицы объема:

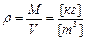
Данное определение конструктивно и позволяет непосредственно производить определение плотности жидкости. Плотность жидких металлов и шлаков изменяется от 2000 кг/м³ до 15000 кг/м³.

Методы измерения плотности.

Для “холодных” жидкостей используются достаточно простые и надежные методы измерения плотности, среди которых: метод простого взвешивания, метод гидростатического взвешивания (в частности, с использованием ареометров), метод максимального давления в газовом пузырьке (или метод Кантора) и др.

Для металлургических расплавов Наибольшее распространение для измерения плотности расплавов получил метод максимального давления в пузырьке, разработанный Кантором.

Метод Кантора основан на использовании закона Паскаля:

P₁ – P₂ = ρ.g.(h₁ –h₂)

где P₁ - давление жидкости на уровне h₁ от поверхности; P₂ - на уровне h₂.

Откуда:

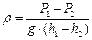
Таким образом, измеряя давления на разной глубине в жидкости, можно рассчитать плотность.

Аппаратура для измерений методом Кантора аналогична аппаратуре для измерения поверхностного натяжения данным методом, приведенной на рисунке 2.13.

Вязкость

В металлургической практике необходимо предвидеть динамические свойства шлака, его способность протекать через отверстия, течь по желобам, вытекать из ковшей, тормозить движение взвешенных в нем капелек металла или штейна. Эти динамические свойства обычно называют текучестью или вязкостью. В отличие от физических свойств, рассмотренных раньше, вязкость в большинстве случаев очень сильно зависит от состава шлаков. Но для того, чтобы сравнивать вязкость различных шлаков, необходимо прежде всего дать его определение и указать методы ее измерения.

Начнем с наших бытовых представлений о вязкости. Прежде всего, мы хорошо знаем, что вязкость - это свойство кинетическое, т.е. мы не можем судить вязкая жидкость или нет, если она находится в покое. Для того нужно, чтобы к жидкости была приложена какая-либо сила, и о вязкости мы судим по тому, насколько сильно жидкость сопротивляется этой силе, стремящейся изменить ее состояние. Для твердых тел такое сопротивление - упругое, т.е. сопротивление возрастает с увеличением деформации сдвига. У жидкости такое сопротивление - неупругое: жидкость начинает течь. Причем чем меньше скорость течения при данной силе, приложенной к жидкости, тем больше ее вязкость. Казалось бы, мы уже готовы дать определение вязкости, но это не совсем так. Дело в том, что скорость течения в жидкости неодинакова во всех ее точках, а зависит еще и от расстояния до стенок емкости, в которой происходит течение. Эксперименты показывают, что изменение скорости V при удалении от стенки на расстояние X (градиент скорости по нормали к поверхности) зависит лишь от силы, приложенной к слою и площади рассматриваемых двух слоев, т.е.:

μ - фактор пропорциональности, который и называют динамической вязкостью или просто вязкостью. Отсюда:

Определение. Динамической вязкостью жидкости называется коэффициент пропорциональности между градиентом скорости движения тонкой пластины единичной площади и силой действующей на эту пластину.

В большинстве книг вязкость приведена в единицах СГС, которой дано специальное название - паузы, обозначается П. Кроме обозначения µ в литературе встречается и другое обозначение динамической вязкости - η.

1 П = 10 Па.с

Кроме понятия динамической вязкости, вводится и понятие кинематической вязкости, представляющей собой отношение динамической вязкости к плотности:

ν = μ/ρ

В СИ единицей измерения η является м²/с.

Вязкость жидких металлов и шлаков в значительной степени зависит от присутствия в них примесей и изменяется в пределах от 0,001 Па.с до 100 Па.с.

Методы измерения вязкости

Методы измерения вязкости более сложные, чем других величин. В таких измерениях обычно используется не определение вязкости, а градуировочные методы. Суть этих методов заключается в том, что сначала строятся градуировочные графики зависимости какой-либо измеряемой величины от вязкости известных жидкостей. После этого определяется та же величина для жидкости с неизвестной вязкостью. Ее вязкость находится по графику.

Для измерения вязкости созданы специальные стандартные приборы - вязкозиметры. Суть некоторых (наиболее распространенных) устройств их устройства заключается в следующем, рисунок 2.14. В емкость с жидкостью опускается цилиндр, одни концом закрепленный на валу электромотора. При включении мотора цилиндр вращается. Мощность, потребляемая двигателем зависит от вязкости расплава. Перед определением вязкости жидкостей необходимо построить градуировочные графики.

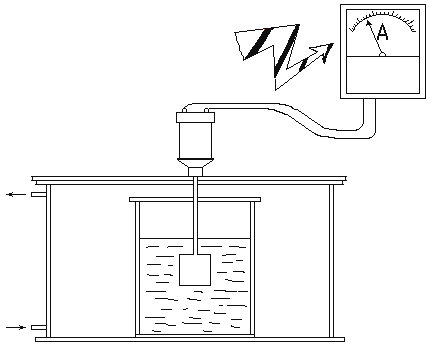
Рисунок 2.14. Схема установки для измерения вязкости жидкости.

<7 8 91011 12 13 >

Дата добавления: 2016-02-09; просмотров: 1834;