Твердое состояние вещества

Твердое состояние вещества характеризуется сохранением формы тела без внешних ограничителей (сосудов) в течение длительного времени. Сохранение формы твердого тела обеспечивается за счет сил взаимодействия микрочастиц, составляющих тело - атомов, ионов, молекул. Важнейшие для практического использования свойства твердых тел значительно различаются в зависимости от состава и внутреннего строения (структуры) тел. В курсе “Основы пирометаллургического производства” и далее в других металлургических курсах вы так или иначе будете сталкиваться с такими важными свойствами твердых тел, как:

· плотность;

· теплопроводность;

· электропроводность;

· скорость диффузионного переноса;

· пластичность;

· коррозионная стойкость и др.

Детально исследование свойств твердых тел и влияния на них различных факторов рассматривается в специальных материаловедческих курсах и курсах, посвященных обработке металлов. Мы в данном разделе в самом общем виде, принципиально, коснемся только некоторых особенностей строения твердых тел, объясняющих основные их свойства (и, прежде всего, металлов).

Химическая связь в кристаллах и элементы зонной теории твердых тел

Природа химической связи рассматривается в курсах физики, химии, физической химии. Поэтому ограничимся лишь напоминанием отличительных особенностей некоторых типов связи, что необходимо для целостности изложения и понимания дальнейшего текста.

Химическая связь осуществляется главным образом силами электрического происхождения, обусловленными взаимодействием внешних электронных оболочек атомов.

В зависимости от характера химической связи все кристаллические тела можно разделить на следующие группы: молекулярные, ионные, ковалентные (атомные) и металлические.

Зонное строение твердых тел подробно рассматривается в курсе физики. В настоящем издании приведены отдельные элементы этой теории.

Положение каждого электрона в атоме отвечает строго определенному квантовому состоянию. В данном квантовом состоянии может находиться лишь один электрон, или эти уровни могут быть не заполнены (принцип Паули).

Электронная конфигурация атомов различных элементов, как известно, записывается следующим образом. Например, натрий: (1s)²(2s)²(2p)⁶(3S)¹.

Электроны в атоме натрия располагаются на разрешенных уровнях в количествах, соответствующих принципу Паули.

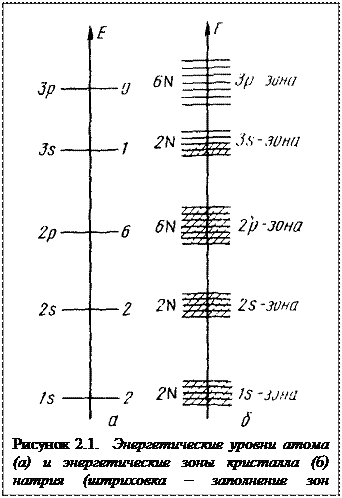
Энергетическое состояние электронов в атоме натрия может быть изображено и другими средствами. На рисуноке 2.1 приведено графическое изображение в условных координатах расположения разрешенных уровней энергии, на которых располагаются электроны.

При образовании из нескольких атомов, того же натрия, твердого кристалла в системе возникают изменения. Сближение отдельных атомов до определенного расстояния вызывает возникновение сил, обеспечивающих взаимное притяжение. Из отдельных атомов образуются молекулы, из молекул твердые тела.

При сближении отдельных атомов на расстояния, на которых начинают проявляться силы взаимодействия между частицами, разрешенные энергетические уровни электронов сосед их атомов претерпевают возмущения, деформируются. При образовании кристалла твердого тела энергетические уровни отдельных атомов образуют энергетическую зону. Зона разрешенных энергий не представляет собой непрерывный спектр энергий. Каждому электрону в этой зоне (в твердом теле количество атомов в 1 см³ равно 10²²) свойственно свое энергетическое состояние, незначительно отличающееся от квантового состояния соседнего атома.

Между разрешенными энергетическими зонами располагается запрещенная зона, которую не могут занимать электроны.

Схематичное графическое изображение образования из атомов натрия твердого кристалла и изменения в структуре энергетических уровней и зон иллюстрирует рисунок 2.1.

Если N атомов образуют кристалл, то, как уже говорилось, вместо дискретных квантовых состояний отдельных атомов образуется энергетическая зона, содержащая N квантовых состояний. В соответствии с принципом Паули в s-состоянии может располагаться не более двух электронов (учитывая различные спины электронов). Таким образом, для заполнения этой энергетической зоны электронами имеется 2N вакантных мест. В зоне p-уровней, соответственно, 6N вакантных мест.

Рассмотрим образование кристалла из атомов натрия (рисунок 2.1). Одноквантовый 1s-уровень превратится в 1s-зону, занимаемую 2N электронами; 1з-зона будет заполнена полностью. То же относится к 2s- и 2р-зонам. В Зs-зоне могут разместиться 2N электронов, но у N атомов Na есть лишь N электронов в состоянии 3s. Следовательно, эта зона заполнена только наполовину. Зоны, лежащие выше, будут совсем не заполнены.

Рассмотрим теперь образование кристалла из атомов лития и фтора (рисунок 2.2). При образовании кристалла из атомов фтора и лития будут полностью заполнены зоны: 1sF, 1sLi, 2sF, 2р-зона фтора имеет 6N вакантных мест для электронов. По у фтора всего 5N электронов в 2р-состояниях. Заполнение электронных оболочек наряду с принципом Паули подчиняется также принципу сохранения системой минимума энергии. Поэтому электроны лития, находящиеся в 2s-состоянии, при наличии свободного места перейдут в зону 2рF, занимающую более низкое энергетическое положение. Количество этих электронов N, общее количество электронов в зоне 2pF-6N. Таким образом, эта зона оказывается заполненной до отказа, а зона 2s остается пустой (рисунок 2.2).

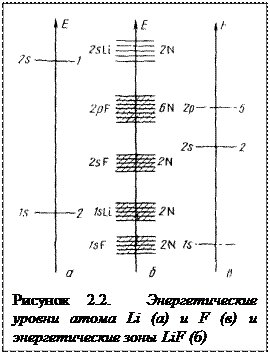Рассмотрим влияние наложения электрического поля на кристаллы. На рисунок 2.3 изображена схема кристалла с неполностью заполненной энергетической зоной.

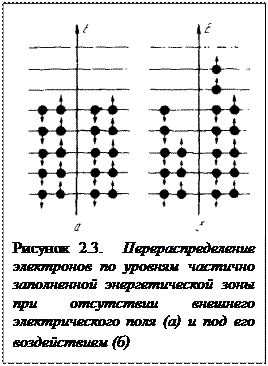
При отсутствии внешнего электрического поля (рисунок 2.3, а) движение электронов хаотично. Такие электроны имеют одинаковые скорости движения во всех направлениях. Приложение внешнего поля (рисунок 2.3, 6) делает движение электронов направленным. В кристалле возникает электрический ток. Сама возможность перемещения электрона при наложении поля обусловлена тем, что имеются очень близкие по энергии вакантные квантовые уровни, поскольку зона не заполнена полностью. Такой случай характерен для металлов.

Совершенно другая картина возникает, если валентная зона оказывается заполненной полностью. Наложение электрического поля в этом случае не приводит к возникновению электрического тока по той причине, что нет вакантных квантовых уровней, куда бы электрон мог переместиться. Хотя следующая разрешенная энергетическая зона (зона проводимости) не заполнена, энергии электрического поля не недостаточно, чтобы возбудить электрон и перевести его в эту незаполненную зону со свободными квантовыми уровнями. Необходимы большие энергии для возбуждения перехода электрона на вышележащие уровни. Величина этой энергии зависит от разности энергий в валентной зоне и зоне проводимости, т.е. от ширины запрещенной ЗОНЫ. Если ширина запрещенной зоны велика, то материал относится к классу диэлектриков (например, такие важные для цветной металлургии вещества, как SiО₂, А1₂O₃, NaCl и др.).

Таким образом, диэлектрики характеризуются полностью заполненной валентной зоной и большой шириной запрещенной зоны.

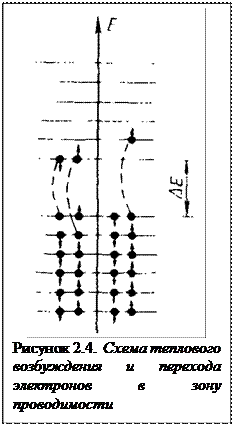
Если энергетический зазор между дном зоны проводимости и верхом валентной зоны невелик, то приложение незначительной внешней энергии, например тепловой, может оказаться достаточной для перехода части электронов из заполненной валентной ЗОНЫ в свободную зону проводимости (рисунок 2.4). Повышение температуры позволяет электронам в ряде соединений преодолеть энергетический барьер запрещенной зоны. В этом. случае зона проводимости оказывается частично заполненной, а в валентной зоне появляются вакантные места электронов. Такие незанятые квантовые состояния электронов называются дырками, которым приписывается положительный заряд. В этом случае приложение внешнего электрического поля к кристаллу вызовет электрический ток, как вследствие перемещения электронов в зоне проводимости, так и дырок в валентной зоне.

Чем больше электронов возбуждено в зону проводимости и, следовательно, чем больше дырок в валентной зоне, тем больше электропроводность такого вещества. Связь между количеством возбужденных электронов n и температурой определяется законом Больцмана:

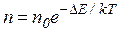
где ∆E — ширина запрещенной зоны, эВ; k= 8,б1б7^.10^-5 постоянная Больцмана эВ/град; n₀ — число электронов в валентной зоне.

Таким образом, чем больше ширина запрещенной зоны, тем более высокая температура требуется для разрушения связей, поскольку энергия пропорциональна величине kT.

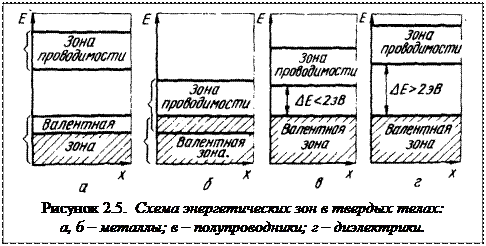
Таким образом, согласно зонной теории твердых тел, различие между металлами (удельная электропроводность æ = 10⁶÷10⁸ Ом^-1м^-1) полупроводниками (æ = 10⁵÷10^-7 Ом^-1м^-1) и диэлектриками (æ = 10^-8÷10^-20 Ом^-1м^-1) связано с разным расположением энергетических зон (рисунок 2.5). На рисунке 2.5а валентная зона не заполнена, на рисунке 2.5 б валентная зона и зона проводимости перекрываются. В обоих случаях существуют незаполненные квантовые уровни, на которые могут переходить электроны практически без затраты энергии. Это обусловливает высокую электропроводность материалов с такой структурой. Зонная структура, приведенная на рисунке 2.5 а и б, характерна для металлов.

Полупроводники характеризуются наличием запрещенной зоны и полностью заполненной валентной зоной. К классу полупроводников условно относятся вещества с шириной запрещенной зоны до 2,5 эВ (рисунок 5 в). Вещества, имеющие ширину запрещенной зоны > 2,5 эВ, относятся к классу диэлектриков (рисунок 5 г).

Зонная структура твердых тел обуславливает особенности и характеристики не только электропроводности, но и теплопроводности твердых тел, поскольку электроны являются переносчиками не только электрического заряда, но и энергии (из физической химии известно, что тепло является формой передачи внутренней энергии). С точки зрения зонной теории твердых тел металлы должны обладать более высокой теплопроводностью, чем полупроводники и тем более диэлектрики. Практические данные по теплопроводности подтверждают данный вывод.

Кристаллическая структура и свойства твердых тел. Дефекты структуры кристаллов

Большинство твердых тел, в том числе и металлы, имеют кристаллическую структуру. Тип кристаллической решетки твердого тела во многом определяет его физические свойства. Например, графит и алмаз – это две разные кристаллические формы (модификации) одного и того же элемента – углерода. Несмотря на то, что химический состав этих веществ полностью идентичен, за счет различий в типе кристаллических решеток физические (и некоторые физико-химические) свойства графита и алмаза различаются значительно (твердость, электропроводность,кинетика окисления и др.). Однако, подобных примеров существования различных типов кристаллической решетки для разных веществ немного. В большинстве случаев для одного и того же вещества в твердом виде (при одной температуре) характерен один тип кристаллической решетки, который во многом определяется строением и свойствами атомов и молекул ее составляющими.

Для металлов характерны типы кристаллических решеток, отличающиеся высокой плотностью упаковки. Во многом благодаря этому (помимо собственных размеров атомов и молекул, входящих в состав кристалла) большинство металлов имеют более высокую плотность по сравнению, например, с неметаллами, или их соединениями с металлами.

С ростом температуры плотность твердых веществ снижается. Связано это с тем, что с увеличением температуры увеличивается амплитуда колебаний атомов (ионов, молекул) в узлах кристаллической решетки, в результате чего возрастает расстояние между ними и, соответственно плотность твердого тела снижается. Коэффициенты температурного расширения металлов как правило выше, чем неметаллов. Коэффициенты теплового расширения твердых тел имеют важное значение для практического использования изделий из твердых тел.

В природе и технике с идеальными кристаллами приходится встречаться редко. Наличие дефектов в кристаллах существенно сказывается на физико-химических свойствах вещества. От наличия дефектов зависят такие свойства твердых тел, как электро- и теплопроводность, механические, химические свойства и т.д. дефекты в кристаллах влияют на термодинамические свойства вещества и кинетику металлургических процессов. Различают следующие два основных вида дефектов в кристаллах: точечные и линейные или плоскостные. Точечные дефекты можно подразделить на атомные (ионные) и электронные.

К атомным можно отнести следующие шесть типов дефектов.

1. Химические примеси. Кристалл с содержанием примеси 0,1 % с химической точки зрения можно считать чистым, но с позиции физики такое содержание будет весьма значительным. Любая точка в подобном кристалле удалена от атома примеси (при равномерном распределении) не более чем на несколько межатомных расстояний. Чужеродные атомы могут быть примесями замещения или примесями внедрения (рис. 2.6).

В качестве примесей следует рассматривать также нарушения в кристаллической решетке соединений, приводящие к искажению симметричной упорядоченности частиц соединений. Влияние этих соединений и чужеродных примесей идентично.

2. Дефект Френкеля. В результате каких-то воздействий атом (ион) из узла решетки может перейти в междузлие с возникновением вакансии в решетке. Этот тип дефекта называется дефектом Френкеля. Он встречается как в элементарных веществах, так и в химических соединениях. В случае химических соединений дефекты Френкеля могут возникать в подрешетке как металла, так и аниона. Не исключена возможность одновременного возникновения дефектов Френкеля в подрешетках металла Ме и аниона Х (анти Френкель):

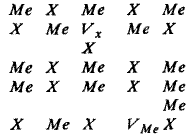Электронейтральность системы и стехиометрические соотношения между катионами и анионами при образовании этого типа дефекта в кристалле не нарушаются.

З. Дефекты Шотки связаны с выходом атома (иона) из узла решетки на поверхность и возникновением в кристалле вакансий. В случае соединения дефекты Шотки могут возникать в подрешетке металла, аниона или одновременно и в той, и в другой подрешетках:

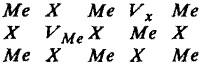
В случае одновременного возникновения вакансий в подрешетках металла и аниона стехиометрические соотношения между компонентами соединения не нарушаются. Образование вакансий одного типа связано с отклонением в стехиометрии соединения и дополнительным возникновением электронных дефектов с сохранением электронейтральности системы дефект анти Шотки — равные количества межузельных атомов М и Х, имеющих одинаковую валентность.

4. Дефект антиструктуры в кристаллах соединений — место катиона в узле решетки занимает анион или наоборот:

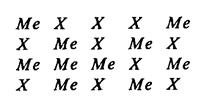
5. Наряду с возникновением перечисленных относительно простых дефектов возможно образование и более сложных комплексных дефектов В частности, при образовании ковалентных связей у атомов серы, селена и теллура друг с другом возможно их сближение вокруг вакансии металла с образованием сложных комплексных дефектов с замыканием связей между отдельными атомами (Например, S-S).

6. Дефектами в кристаллах следует считать наличие электронов в зоне проводимости и дырок в валентной зоне дефекты такого рода характерны для диэлектриков и полупроводников.

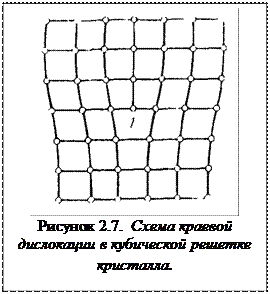К линейным или плоскостным дефектам кристаллической структуры следует отнести различные виды дислокаций (дислокация — это область в кристалле, в которой нарушена периодичность кристаллической решетки). Плотность дислокаций в металлических кристаллах находится в пределах 10⁴-1О⁶ на каждый квадратный сантиметр. Простейшими типами дислокаций являются винтовая и краевая дислокации На рисунке 2.7 приведена схема краевой дислокации (1) в кристаллической решетке. Дислокации возникают в результате неправильного роста кристаллов или при термической и механической обработках.

Дефекты кристаллической решетки оказывают большое влияние на механические, электрофизические свойства кристаллов (кристаллических веществ), кинетику металлургических процессов. Например, присутствие даже небольших количеств (0,1-1 %) серы, свинца, мышьяка, сурьмы в меди в несколько раз (и даже на порядки) ухудшает такие важнейшие свойства меди как электропроводность, теплопроводность, пластичность, коррозионная стойкость и др., и во многом это связано с возникновением различных дефектов в кристаллической структуре металла.

Далеко не всегда те или иные изменения в кристаллической структуре металла, связанные с присутствием примесей, оказывают негативные воздействие на все свойства металла. Например, добавка небольших количеств меди, марганца и магния к алюминию приводит к значительному увеличению его прочности, что позволяет расширить диапазон применения алюминия.

Диффузия в твердых телах

Металлургам обычно приходится иметь дело с реакциями, протекающими в гетерогенных системах. Во многих случаях скорость протекания процесса лимитируется скоростью процессов массообмена и в том числе скоростью молекулярной диффузии. В свою очередь скорость процесса диффузии в твердых телах зависит от структуры дефектов, а изучение закономерностей массообмена дает ценную информацию о природе дефектов. Общие закономерности диффузионного перемещения частиц в веществе определяются законами Фика.

При наличии градиента концентрации какого-либо вещества вдоль оси Х возникает поток П, который пропорционален градиенту концентрации дс. Это первый закон Фика:

П = - D^.дс/дx

где: D — коэффициент пропорциональности или коэффициент диффузии, см²/c.

Если исчезнет градиент концентрации, исчезнет и поток компонентов вдоль оси.

Если стационарное состояние не достигнуто, т.е. концентрация компонента меняется в каждой точке в зависимости от времени, первый закон Фика удобнее выражать в дифференциальной форме:

дс/дt = — D^.(д²с/дx²)

Уравнение представляет собой второй закон Фика. Коэффициент диффузии D различен для разных веществ и даже для одного и того же вещества в сильной степени зависит от структуры дефектов и их концентрации. Эта характеристика не является постоянной величиной для всей области гомогенности существования данного вещества или твердого раствора.

Атомы и ноны могут диффундировать в твердом теле по различному механизму. В литературе рассматриваются четыре различных варианта механизма диффузии в твердых телах.

1. Межузельный механизм. Можно предположить, что атом (ион) диффундирует из одного положения в другое по межузлиям, не вызывая смещения атомов матрицы. Прежде чем атом 1 (рис. 2.8, а) может перейти в состояние 2, атомы З и 4 должны раздвинуться, чтобы дать ему возможность провести перемещение. Такое расширение атомов, или искажение решетки, требует затраты энергии Считается, что такой механизм доминирует в сплавах, в которых посторонние атомы образуют раствор внедрения и атомы примеси по размерам существенно отличаются от атомов матрицы.

2. Вакансионный механизм. Пусть в плотно упакованной гранецентрированной решетке имеется вакансия (см. рисунок 2.8, 6). Казалось бы, при этом энергия, которую необходимо затратить на переход атома в вакансию, сравнительно невелика (так же как и в предыдущем случае, энергия должна быть затрачена на искажение решетки). Исходя из этого, следовало бы ожидать высоких коэффициентов диффузии. В действительности же коэффициенты диффузии при вакансионном механизме нередко меньше, чем для случая межузельной диффузии.

З. Диффузия по межузлиям путем вытеснения (обменный механизм). Примесные атомы, образующие растворы внедрения, обычно по размерам заметно меньше, чем атомы металла—растворителя. Если внедренные атомы близки по размеру к атомам растворителя, то переход таких больших атомов из одного межузлия в другое будет сопряжен с большими затратами энергии, с серьезным искажением решетки диффузии в этом случае может происходить путем выталкивания внедренным атомом одного из ближайших соседей в соседнее межузлие (см. рис. 2.8, в).

Атом 1, находящийся в межузлии, выталкивает с мест “хозяина” атом 2 и занимает его место. Атом 2 перемещается в ближайшее межузлие (положение 3).

4. Кольцевой .механизм. Самодиффузия частиц в кристаллах может осуществляться по кольцевому механизму (см рис. 2.8). При этом для перемещения одной частицы требуется большая затрата энергии на искажение решетки Если же в движение вовлекаются 2—3 частицы или более, то затрата энергии будет значительно меньшей.

Приведенные варианты механизмов диффузии тесно связаны со строением твердого тела. Так, чем большее количество вакансий имеется в твердом теле, тем легче и быстрее должна осуществляться диффузия частиц, тем с большей скоростью будут протекать металлургические процессы.

Оценку тому или иному механизму диффузии в твердом теле можно дать на основании изучения зависимости диффузии от температуры:

D=D₀exp(-E/RT)

(D — коэффициент диффузии, м²/c; D₀ — предэкспоненциальный фактор, характеризующий величину коэффициента диффузии при высоких температурах, м²/c; Е — энергия активации диффузии, величина, определяющая высоту потенциального барьера, который надо преодолеть частице, чтобы перейти из одного положения в решетке в соседний узел или межузлие, кДж/моль)

Величины Е и Р можно найти аналитическим или графическим путем по экспериментальным данным. Температурной зависимости коэффициента диффузии золота в серебре соответствует выражение: D = 5,3^.10^-8.exp(124862/8,31^.Т), м²/c; D₀ = 5,3^.10^-8 м²/c; Е = 125 кДж/моль.

Так как lnD = lnD₀ — Е/RТ, то, продифференциировав последнее выражение, получим dlnD/d(1/Т) —Е/R, из которого определим Е при известных Т и D. Подставляя значение Е в предыдущую формулу, можно определить D₀.

Величины Е и D₀ определяются и из графической зависимости. Очевидно, тангенс угла наклона прямой в осях lnD -1/Т будет равен Е/R, а отрезок на оси ординат при 1/Т =0 соответствует lnD₀.

Наиболее совершенным методом определения коэффициентов диффузии является метод определения изменения концентра диффундирующего вещества о времени в толще образца с использованием радиоизотопов.