Вещество в газообразном состоянии.

В пирометаллургических процессах, как уже отмечалось на предыдущих лекциях, обязательным продуктом являются отходящие газы. Газы образуются из компонентов исходного сырья при их нагревании (вода, CO₂ карбонатов и т.д.), из компонентов, образующихся в результате протекания многочисленных окислительно-восстановительных реакций (SO₂, CO, CO₂, H₂O, SO₃, NO₂, NO и др.) и из компонентов подаваемых в пирометаллургический аппарат газообразных реагентов (кислородсодержащего дутья, природного газа, синтетических газовых реагентов и т.д.). Параметры газовой фазы играют важнейшую роль в протекании физико-химических взаимодействий, определяют характеристики важнейшей системы современного пирометаллургического комплекса – системы охлаждения и очистки газов. Поэтому, безусловно, квалифицированный металлург должен уметь рассчитывать параметры газов применительно к условиям металлургического процесса, анализировать и рассчитывать физико-химические процессы, протекающие в газовой фазе и с участием газовой фазы.

Общие определения и свойства.

Газообразное состояние вещества характеризуется значительно (на несколько порядков) более высокими расстояниями между молекулами, в результате чего силы межмолекулярного взаимодействия становятся настолько малыми, что не позволяют удержать газ в пределах определенной формы и объема. Форма и объем газа полностью определяются формой и объемом сосуда, в котором он находится.

В подавляющем числе случаев при анализе и расчетах характеристик газовой фазы в пирометаллургических процессах пользуются понятием идеальный газ и применят законы, полученные для таких газов.

Идеальный газ – это такое состояние вещества, при котором расстояния между молекулами настолько велики, что потенциальная энергия взаимодействия между молекулами исчезающее мала по сравнению с их кинетической энергией, и можно пренебречь собственным объемом молекул по сравнению со всем объемом, занимаемым газом.

Безусловно, идеальный газ это гипотетическое состояние, однако, при достаточно высокой температуре и большом объеме любой газ будет вести себя как идеальный. В большинстве случаев условия пирометаллургических процессов соответствуют этому. Только при очень высоком давлении (в несколько десятков атмосфер) и (или) очень низкой температуре, близкой к абсолютному нулю, поведение газов будет отличаться от законов идеального газа. Такие газы называют реальными.

Из кинетической теории газов известно, что поведение идеального газа подчиняется уравнению Клапейрона—Менделеева:

pV= nRТ

где: n - число молей газа в объеме; R-универсальная газовая постоянная, равная 0,08205 л ^. атм./(К^.моль) или 8,314 Дж/(К^.моль); Т - абсолютная температура, К.

Приведенное выше уравнение называют уравнением состояния идеального газа, поскольку оно связывает основные параметры его состояния – температуру, объем и давление.

Уравнения состояния реальных газов сложны, громоздки и практически индивидуальны для каждого газа. Для сохранения форм описания реальных газовых систем такими же, какие используются для идеальных газов, вводят функцию, называемую фугитивностью f или летучестью, которая рассматриваемая как исправленное давление. Проблемы отклонений свойств реальных газов от свойств идеальных газов сводятся к нахождению этой величины. Другими словами фугитивностью называют такую величину, которая связана с другими термодинамическими характеристиками реального газа так же, как с ними связано давление в случае идеального газа. Таким образом, уравнение состояния для реального газа выглядит:

fV= nRТ

Для идеальных газов фугитивность равна давлению.

Из уравнения Клапейрона-Менделеева, в частности, следует, что объем 1 моля идеального газа при нормальных условиях (давление 1 атм., температура 0 °С) равен 22,4 л.

В пирометаллургических процессах происходит значительный нагрев исходных газовых реагентов и газов образующихся в процессе. Так, если исходная температура подаваемых в печь веществ часто составляет не более 20-30 °С, то температура отходящих газов пирометаллургического агрегата достигает 1000-1700 °С. В соответствии с уравнением () объем газов при нагревании возрастает в 3-6 раз, что безусловно необходимо учитывать при разработке и эксплуатации металлургического процесса.

Плотность газов.

Как известно плотность равна:

ρ = M/V

где: M – масса вещества; V – объем.

Согласно основному уравнению состояния идеального газа объем 1 моля идеального газа равен:

V₀ = RT/p

Тогда для плотности идеального газа может быть записано выражение:

ρ = μ^.p/RT

где: ρ – плотность, кг/м³; µ - кг-моль, кг; p – давление, атм.; R-универсальная газовая постоянная, равная 0,08205 л ^. атм./(К^.моль); Т - абсолютная температура.

Плотность газа прямо пропорциональна давлению и обратно пропорциональна абсолютной температуре.

В частности, для нормальных условий плотность идеального газа равна:

ρ = μ/22,4

Например, кг-моль кислорода равен 32 кг, плотность кислорода при нормальных условиях составит 32/22,4=1,4286 кг/м³. При давлении p и температуре T плотность кислорода будет равна ρ = 1,4286^.p^.273/T.

Для плотности идеального газа сложного состава справедливо выражение:

ρ = Σρ_iN_i

где: ρ_i – плотность i-го компонента, кг/м³; N_i – мольная доля i-го компонента.

Теплосодержание газов.

В практике пирометаллургических процессов важнейшее значение имеет тепловой баланс, неотъемлемой частью которого является расход тепла на нагрев газовых реагентов и продуктов. Расчет теплосодержания (или энтальпии) газов связан с понятием теплоемкости, значения которой зависят от условий процесса. Рассмотрим различные условия нагрева газов.

Изохорический процесс. Это процесс, протекающий при постоянном объеме. При подводе тепла к газу в этих условиях происходит увеличение температуры и давления(уравнение ()). Согласно первому закону термодинамики тепло, подводимое газу тратится на изменение его внутренней энергии и совершение газом работы:

δQ = dU + δA= dU + pdV

Поскольку при постоянном объеме dV=0, то:

δQ_V = dU или

Q_V=∆U=U₂-U₁

Это означает, что при изохорическом процессе все тепло, подводимое к системе, идет только на увеличение ее внутренней энергии. Отсюда вытекает выражение для молярной теплоемкости при постоянном объеме С_V. Согласно уравнению () и определению теплоемкости:

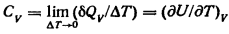
Сопоставляя уравнения, можно заметить, что теплоемкость при постоянном объеме характеризует возрастание внутренней энергии.

Для идеального газа (дU/дV)_T=0, и поэтому в выражении для С_V можно заменить частную производную полной, т. е.

C_V=dU/dT

Увеличение внутренней энергии тела при его нагревании от Т₁ до Т₂ (как и количество тепла на нагрев газа) определяется величиной интеграла:

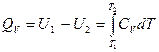
Для того чтобы найти численное значение интеграла, необходимо знать вид функциональной зависимости С_V от T.

Здесь и дальше большая буква С обозначает теплоемкость одного моля вещества.

Изобарический процесс. Это процесс, протекающий при постоянном давлении. При постоянном давлении выражение первого закона термодинамики можно записать в виде:

δQ_p = dU + d(pV) =d(U + pV)=dH

Таким образом, тепло, придаваемое системе при постоянном давлении, расходуется на приращение некоторой функции Н=U+PV, которая называется энтальпией или теплосодержанием. Энтальпия, как и внутренняя энергия, является функцией состояния. Ее изменение не зависит от пути процесса, так как изменения P и V определяются только начальным и конечным состояниями. Из уравнения (_) следует, что

δQ_p = dH или

Q_p=∆H=H₂-H₁

Из уравнений видно, что в двух частных случаях (при постоянных объеме или давлении) количество тепла, сообщенное системе, равно изменению величин функции состояния U или H. Иными словами, тепловые эффекты подобных процессов полностью определяются начальным и конечным состояниями системы. Обычно функция Н используется чаще, чем функция U, так как большинство реальных процессов протекает при постоянном давлении.

Изменение энтальпии характеризует количество тепла, сообщенного системе при изобарическом процессе. На этом основании можно определить теплоемкость при постоянном давлении уравнением

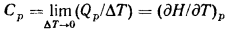
Соответственно, в системах с постоянным давлением:

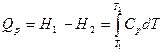
Последнее выражение позволяет определить необходимые затраты тепла на нагрев газа в системах с постоянным давлением (наиболее часто встречающиеся в пирометаллургии) при известной зависимости 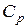от температуры. Эти зависимости для большинства газов можно найти в таблицах термодинамических данных. Как правило они приводятся в виде полиномов: 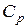=a₀+a₁^.T+a₂^.T²+…., которые легко могут быть проинтегрированы.

Если С_p не зависит от температуры (слабо зависит), то:

Q_p = C_p ^.(T₂-T₁)

Теплоемкость при постоянном давлении выше, чем при постоянном объеме, поскольку в изобарических процессах передаваемое газу тепло затрачивается не только на его нагрев (увеличение температуры, являющейся характеристикой кинетической энергии газовых молекул), но на совершение работы по расширению газа при нагревании. Уравнения позволяют вычислить разность между молярными теплоемкостями при постоянных объеме и давлении для идеального газа. В этом случае величина С_V может быть выражена через полную производную dU/dТ. Величина Н для идеального газа также не зависит от давления, а только от температуры, так как произведение рV при данной температуре постоянно. Таким образом, учитывая, что Н=U+рV, находим

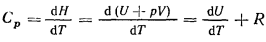
откуда следует, что

С_p-C_V=R

т. е. теплоемкость одного моля идеального газа при постоянном давлении больше теплоемкости при постоянном объеме на величину, равную R, т. е. 8,314 Дж/(моль^.К) или 1,987 кал/моль^.К. Молярная теплоемкость одноатомных газов (благородные газы, пары некоторых металлов) при постоянном объеме равна 12,071 Дж/(моль^.К). Из уравнения (_) следует, что для таких газов С =12,071+8,314=20,385 Дж/(моль^.К). Отметим, что полученное выражение разности теплоемкостей справедливо только для идеальных газов и не выполняется для реальных азов.

Из уравнения Клапейрона-Менделеева и выражения работы, как произведения рV, следует, что величина R есть работа расширения моля идеального газа при нагревании на 1К при постоянном давлении. Отсюда можно вычислить механический эквивалент тепла, приравняв разность теплоемкостей Сp и Сv выраженную в тепловых единицах, к работе расширения газа в механических единицах. Например, разность С выраженная в калориях, есть 1,987 кал/ /(моль^.К), а в джоулях она равна 8,314. Отсюда калория эквивалентна 8,314/1,987==4,184 Дж. Подобный расчет впервые был сделан в 1842 г. одним из основателей первого закона термодинамики Р. Майером.

При нагревании твердых тел работа расширения незначительна по сравнению с изменением внутренней энергии. Поэтому С_p-C_V для твердых тел меньше, чем для газов. Обычно она составляет 0,8+1,2 Дж/(моль^.К) и определяется не только работой, но и изменением внутренней энергии при изменении объема.

Если С_p не зависит от температуры (слабо зависит), то тепло, необходимое на нагрев газов при постоянном давлении можно рассчитать по упрощенной формуле:

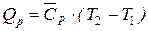
где: 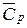- средняя теплоемкость в диапазоне температур T₁÷T₂.

Теплоемкость газов зависит от их состава. При прочих равных условиях чем больше атомов в молекуле газа тем выше его молярная теплоемкость.

Для теплосодержания идеальных газов справедливо правило аддитивности, т.е. теплосодержание газовой смеси равно сумме теплосодержаний всех компонентов газовой смеси.

Другие свойства газов.

Несколько подробнее мы рассмотрели два свойства газов (идеальных газов) с которыми вам придется сталкиваться несколько чаще в металлургических курсах и в курсе “Основы пирометаллургических процессов”, в частности. Помимо рассмотренных свойств для анализа процессов тепло- и массопереноса в системах с газовой фазой используются такие свойства газов, как теплопроводность, степень черноты, вязкость и др. Эти свойства газов подробно рассматриваются в курсах тепломассопереноса.

В теории и практике металлургии часто используются такие понятии как окислительные и восстановительные свойства газовой фазы, окислительный потенциал газовой фазы, сульфидирующий потенциал газовой фазы. Однако, эти понятия не являются общепринятыми и в разных источниках определяются по-разному. Чаще всего, эти понятия отражают особенности состава газовой фазы по содержанию в ней кислорода, серы, водорода и др., т.е. являются характеристиками состава газовой фазы. В частности, в работах по цветной металлургии распространенным является использование в качестве характеристики окислительных свойств газовой фазы величины парциального давления кислорода p_O2, в качестве характеристики сульфидирующих свойств потенциала – парциального давления серы p_S2, называемого иногда сульфидирующим потенциалом, а в качестве характеристики восстановительных свойств газа – отношение CO/CO₂. При исследовании и анализе металлургических процессов эти показатели могут определяться экспериментально либо рассчитываться с использованием балансовых, термодинамических или кинетических закономерностей. Примеры подобных расчетов и анализов мы с вами рассмотрим на практических занятиях и в лекциях, посвященных термодинамике металлургических систем.

Жидкое состояние вещества. Физические свойства жидкостей. Плотность. Молярный объем. Вязкость. Поверхностное натяжение. Физико-химические свойства растворов. Активность. Коэффициент активности. Предельные законы. Модели растворов