Физико-химические свойства растворов. Активность. Коэффициент активности. Предельные законы. Модели растворов.

Растворы

В металлургии подавляющее число процессов протекает с участием растворов. Химически чистые вещества представляют собой лишь предельное состояние, которое никогда в действительности не наступает. Даже самые чистые вещества, получаемые в современной технике, все же содержат некоторое количество примесей, главным образом металлоидов, и по существу являются растворами.

Чаще всего в пирометаллургии имеют дело с жидкими растворами (расплавами). Расплавы чугуна, стали в черной металлургии являются растворами различных элементов в железе. В цветной и черной металлургии получают шлаки - растворы окислов, штейны - растворы сульфидов и т.д. В гидрометаллургических процессах для извлечения цветных металлов используются растворы солей, кислот, оснований.

Вспомним некоторые базовые понятия и определения из физической химии, связанные с растворами.

Растворомназывается однородная смесь, состоящая из двух или большего числа веществ, состав которой в известных пределах может меняться.

Однородными являются и химические соединения, однако их состав не может изменяться непрерывно, т.к. они подчиняются законам постоянства состава и кратных соотношений.

При образовании раствора компоненты взаимодействуя друг с другом в растворе теряют свою индивидуальность. Свойства раствора могут быть охарактеризованы термодинамическими характеристиками V, H, U, F, G и т.д. Вследствие взаимодействия между молекулами компонентов раствора термодинамические характеристики имеют смысл относить к раствору как к целому, а не к составляющим его веществам. Так, раствор характеризуется вполне определенным, поддающимся измерению объемом, однако нельзя определить, какие объемы занимают в нем отдельные компоненты. В растворе наряду с энергией взаимодействия между молекулами одного и того же компонента существует и эн. взаимодействия между молекулами различных компонентов раствора и отнести ее можно только к раствору в целом. Однако, важно охарактеризовать, какую долю вносит данный компонент в то или иное свойство раствора. Такая характеристика носит название парциальной молярной величины.

Большинство поддающихся измерению свойств может быть разделено на две группы:

* интенсивные ® не зависят от кол-ва в-ва (температура, давление)

* экстенсивные ® зависят от количества в-ва (объем, масса, U, G, H, S и т.д.).

Величины интенсивных свойств в различных частях системы стремятся к выравниванию.

Г Льюис назвал парциальной мольной величиной компонента частную производную от какой-либо экстенсивной величины gпо числу молей n_i этого компонента р-ра при постоянных давлении, температуре и числе молей остальных компонентов.

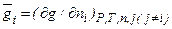
Соблюдение условий, требуемых этим определением, может быть достигнуто, если, например, к весьма большому объему раствора данной концентрации при постоянных P_общ. и T добавить 1 моль какого-либо компонента.

Например, парциальный мольный объем определяется уравнением:

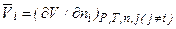
Если р-р образуется из компонентов без изменения объема, то, очевидно. что парциальный мольный объем равен его мольному объему, т.е.

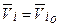
где (_o) означает, что вещество находится в чистом состоянии.

В отличие от мольного объема величина парциального мольного объема может быть даже отрицательной, если вследствие сильного взаимодействия при добавлении компонента происходит уменьшение объема раствора.

Если при образовании раствора соблюдается аддитивность, то свойство раствора может быть выражено:

g = n₁g_1o + n₂g_2o +.....+ n_ig_io

где g_io - мольные свойства чистых веществ; n_i - кол-во молей i-го компонента.

Очевидно, что в этом случае Dg = 0, т.е. образование раствора происходит из чистых компонентов без изменения свойства g.

Если, например, при образовании раствора энтальпия аддитивна, то DH = 0 и раствор образуется без теплового эффекта. Если H исходных веществ > H раствора, при его образовании происходит выделение тепла. В противоположном случае - поглощение тепла.

Среди парциальны мольных величин особое значение имеет парциальная мольная свободная энергия:

которая также часто называется химическим потенциалом - m_i

Хим. потенциал, наряду с T и P является интенсивной величиной.

Равенство температур, давлений и хим. потенциалов всех компонентов в различных частях системы выражает условия термического, механического и химического равновесий.

_

Величина G_i = m_i отражает тенденцию в-ва покинуть данную фазу и является мерой его рассеиваемости.

Раствор - пар. В равновесии:

При 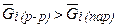- испарение из раствора i - го компонента.

При 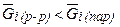- конденсация и переход в раствор i - го компонента.

Пусть пар - идеальный газ. Тогда хим. потенциал i-го компонента в газе равен мольной свободной энергии этого компонента в газе при давлении, равном его парциальному давлению в смеси, т.е.:

m_{i (газ)} = = L_i(T) + RT ln P_i

В равновесии: m_{i (р-р)} = m_{i (газ)} = L_i(T) + RT ln P_i

Обозначив L_i(T) как m_{i o} получим: m_{i (р-р)} = m_{i o} + RT ln P_i , т.е. хим. потенциал компонента в р-ре связан с его парциальным давлением над раствором в равновесии.

Идеальные растворы

Цель термодинамической теории растворов - связать различные свойства растворов и найти способы их расчетов исходя из свойств чистых компонентов. Из-за очень сложного характера взаимодействия компонентов в растворе решение поставленной задачи в общем виде пока невозможно. Поэтому при описании систем с растворами пользуются теми или иными приближениями, на основе некоторых идеализированных представлений о растворах. На сегодняшний день известно большое кол-во самых различных подходов к описанию свойств растворов, реализованных в виде некоторых расчетных схем - моделей, многие из которых весьма сложны и требуют применения достаточно мощной вычислительной техники. Из всего количества видов идеальных растворов, известных на сегодняшний день, мы рассмотрим 2 наиболее известных и простых типа идеальных растворов:

* бесконечно разбавленные (или просто разбавленные) растворы, (далее б.р.р.);

* совершенные растворы.

Бесконечно разбавленные растворы (брр)

Пусть индекс 1 - относится к растворителю, а индекс i (1,2,3, ...) - к растворенному веществу. Тогда:

Бесконечно разбавленный раствор - это такой раствор, в котором N₁ ® 1, а N_i ® 0 (N - мольная доля)

Особенностью такого раствора является то, что молекулы растворенного вещества отделены друг от друга большим числом молекул растворителя. Поэтому в таком растворе имеет место только взаимодействие между растворенным веществом и растворителем, и отсутствует взаимодействие между молекулами растворенного в-ва.

Между веществами в состоянии бесконечно разбавленного раствора и в состоянии идеального газа существует определенная аналогия. Отсутствие взаимодействия в разбавленном растворе между молекулами растворенного вещества приводит к тому, что как и в идеальном газе, концентрация растворенного в-ва не влияет на величину внутренней энергии растворенного вещества (в расчете на моль), т. е. при T=const. парциальная внутренняя энергия постоянна. По той же причине не зависит от состава и парциальная мольная энтальпия растворенного вещества (т.к. взаимодействие с растворителем такое же. как и при добавлении в чистый растворитель.

Давление пара растворенного в-ва

Одним из важных факторов, определяющим растворимость газов в жидкостях, является давление их парциальное давление. Согласно закону, найденному Генри опытным путем, при постоянной температуре кол-во растворенного газа в данном объеме растворителя пропорционально парциальному давлению газа:

C₂/p₂ = г₂ и С₂ = г₂ *p₂

г₂ - постоянная Генри

Это уравнение позволяет рассматривать закон Генри как описание зависимости парциального давления растворенного вещества над бесконечно разбавленным раствором от его концентрации. Т.к. в разбавленном растворе все концентрации пропорциональны друг другу, то закон Генри справедлив при любом способе выражения концентрации.

Существенно, что это уравнение справедливо, если вещество не меняет своей молекулярной массы при растворении.

Например, в водном растворе азот растворяется

N_2(газ) = N_{2 (р-р)} и С_N2 = г_N2 * p_N2

Но в металле азот растворяется в атомарном виде и в этом случае:

, т.е.

растворимость двухатомных газов в металлах пропорциональна не их парциальному давлению, а корню квадратному из этой величины. Этот факт известен как закон Сивертса.

Вообще растворение газа A в конденсированной фазе можно рассматривать как реакцию:

А_(газ) = А _(р-р)

константа равновесия которой К_р = С_А/р_А является величиной, равной константе Генри К_р = г_А. Величина г_А называется также коэффициентом растворимости, т.к. она численно равна растворимости при давлении 1 атм.

Константа Генри описывает равновесие газ-раствор и поэтому должна зависеть от T по тому же закону, что и константа равновесия:

d(lnK_p)/dT = DH/RT²

DH - изменение энтальпии при растворении.

Если DH < 0, т.е. растворение идет с выделением тепла (растворение газов в обычных жидкостях) - с ростом T растворимость газов (при данном давлении) будет снижаться.

При растворении газов в металлах обычно тепло затрачивается, во-первых. на диссоциацию молекул, во-вторых, на раздвижение плотноупакованных атомов металла при растворении, что не компенсируется энергией растворения. Поэтому, как правило, DH растворения газов в металлах > 0, т.е. идет с поглощением тепла и растворимость газов в металлах растет с увеличением температуры.

Давление пара растворителя

Рауль эмпирическим путем установил, что давление пара растворителя над раствором равно давлению пара над чистым растворителем, умноженным на его мольную долю в растворе, т.е. давление пара растворителя над раствором ниже, чем над чистым растворителем.

P₁ = P_1o*N₁

В отличие от закона Генри, где г не имеет простого смысла, в законе Рауля коэффициент пропорциональности между концентрацией и парциальным давлением есть величина обратная давлению пара чистого растворителя:

N₁ = P₁ /P_1o

Кроме того, закон Генри справедлив при любом способе выражения концентрации, а закон Рауля требует, чтобы она выражалась в мольных долях.

Оба закона справедливы для разбавленных растворов

Т.к. давление пара чистого растворителя больше, чем его давление над раствором, то раствор и чистый растворитель не могут быть в равновесии. Наличие растворенного в-ва снижает тенденцию растворителя к испарению.

Закон действующих масс для разбавленных растворов

Для растворенных веществ по аналогии с идеальными газами при пост. температуре константа реакции, например:

А _(р-р) + В _(р-р) = 2D _(р-р)

K = C_D²/(C_A *C_B) = пост. (легко выводится, записав K_p для реакции в газовой фазе и выразив P_A,B,D через C_A,B,D и соответствующие константы Генри).

Закон распределения.

Рассмотрим распределение растворенного в-ва между двумя фазами, если вещество в обоих фазах находится в состоянии б.р.р.

В равновесии 2 конденсированные фазы и пар устанавливаются концентрации i-го компонента в первой и второй фазах соответственно C_i1 и C_i2 и давление P_i. Согласно закону Генри:

C_i1 = г_i1* P_i и C_i2 = г_i2* P_i

Легко получить:

C_i1/ C_i2 = г_i1/г_i2 = const, = L

Эту величину называют коэффициентом распределения, который для данного раствора и растворенного в-ва зависит только от T и не зависит от C_i в фазах. Этим коэффициентом часто пользуются при расчетах распределения малых элементов (примесей) между металлургическими продуктами. Как и константа равновесия L зависит от температуры:

d(lnL)/dT =DH/RT²

DH -изменение энтальпии при переходе растворенного в-ва из второй жидкости в первую.

Пример: закон распределения используют для описания распределения:

* серы между шлаком и сталью (в черной металлургии),

* As, Zn, Pb и др. между штейном и шлаком (в цветной металлургии).

На использовании закона распределения основана зонная очистка металлов.

Совершенные растворы

В металлургии, часто применяют концентрированные растворы, например, штейны, шлаки, сплавы. Поэтому необходимо знание термодинамических свойств таких растворов. В первую очередь зависимости химического потенциала компонента от состава раствора. Для этого сначала рассмотрим идеализированный раствор, в котором компоненты очень близки по своим физико-химическим свойства. Более или менее подобны таким растворам, например, расплавы близких по своей природе веществ Fe-Ni, FeO-МnO.

Растворы, образованные близкими по свойствам компонентами, называются совершенными.

Совершенные растворы характеризуются благодаря близости свойств компонентов тем, что они образуются без теплового эффекта и без изменения объема (ΔН=0, ΔV=0). Вследствие этого, например, в случае бинарного раствора, содержащего n₁молей первого компонента и n₂ второго, энтальпия Hи объем V выражаются уравнениями:

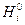где: и , соответственно, объем и энтальпия чистых веществ.

Это означает, что совершенные растворы подчиняются правилу аддитивности.

Так как для совершенного раствора ΔН=0, то из уравнения ΔG=ΔН-T^.ΔS следует, что ΔG=-T^.ΔS, т е. тенденция к образованию такого раствора определяется только увеличением энтропии (без химического взаимодействия между компонентами раствора, поскольку внутренняя энергия и энтальпия при этом не меняются). Отсюда также следует, что в отличие от величин Hи V энергия Гиббса и энтропии при образовании совершенного раствора неаддитивны. Очевидно, энтропии раствора определится уравнением:

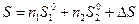
где ΔS - энтропия смешения.

Другие свойства совершенных растворов.

· совершенный раствор образуется всегда самопроизвольно при любых концентрациях;

· изменение энтропии при образовании 1 моля бинарного совершенного раствора равно:

· Химический потенциал компонента совершенного раствора равен:

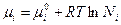
· В совершенных растворах все компоненты подчиняются одному закону – закону Рауля, т.е.:

Из этого следует, что давление пара над раствором, как отдельных компонентов, так и суммарное давление, линейно зависят от состава раствора, что иллюстрируется диаграммой давление-состав, приведенной для бинарного раствора на рисунке 2.15.

Рисунок 2.15. Влияние состава совершенного раствора на давление паров над раствором

· Закон действующих масс для совершенных растворов справедлив при подстановке в его выражение мольных долей участвующих в реакции компонентов. Например, для реакции с участием компонентов совершенного раствора A_р-р=2B_р-р закон действующих масс запишется в виде

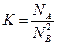
Реальные растворы, вообще говоря, не обладают свойствами совершенных растворов. Часто для качественного анализа поведения компонентов в растворе сравнивают их поведение с совершенным раствором, отмечая положительные или отрицательные отклонения в таком поведении от идеального (совершенного) раствора. На рисунке 2.16 приведены зависимости давления пара от состава для двух реальных растворов. Прямые штриховые линии соответствую давлению пара, которое наблюдалось бы, если бы растворы были совершенными.

а б

Рисунок 2.16. Положительные (а) и отрицательные (б) отклонения от законов Рауля. Касательные к кривым указывают области концентраций, в которых выполняются законы Рауля и Генри

Наличие положительных отклонений показывает, что образование раствора затруднено по сравнению с совершенным. При больших положительных отклонениях жидкости расслаиваются. Отрицательные отклонения указывают на более сильную тенденцию к образованию раствора по сравнению с совершенным. Это означает, что имеются дополнительные причины, облегчающие образование раствора.

Помимо бесконечно разбавленных и совершенных растворов существуют и другие идеальные растворы, в основу которых положены те или иные идеализированные представления о строении или свойствах растворов. К таким растворам относятся, например, регулярные растворы, для которых принято, что энтальпия их образования, в отличие от совершенных растворов, не равна нулю (т.е. растворы образуются с тепловым эффектом), а энтропия смешения рассчитывается также, как и для совершенных растворов.

Активность

Как все в нашей жизни реальное положение вещей отличается от идеальных представлений, так и реальные растворы не обладают свойствами рассмотренных выше идеальных (разбавленных и совершенных) растворов. В подавляющем большинстве случаев соотношения для идеальных растворов не могут быть непосредственно использованы для расчетов равновесий, в которых участвуют реальные растворы. В частности, один из основных законов химии - закон действующих масс не выполняется в реальных растворах, т.к. константа равновесия оказывается непостоянной и зависит от концентрации.

Для расчета равновесий возникла необходимость введение такой характеристики, которая позволяла рассчитывать показатели реальных систем и для сохранения вида уравнений, полученных для идеальных условий, удовлетворяла бы следующим требованиям:

1) через нее должны просто удовлетворяться все термодинамические свойства растворов;

2) в предельных случаях (для идеальных растворов) она должна совпадать с концентрацией, а в реальных растворах показывать степень их отклонения от идеальности;

3) с ее помощью желательно сохранить форму уравнений, выражающих законы идеальных растворов.

В качестве такой характеристики выбрана характеристика названная термодинамической активностью a. Сохраняя форму записи для химического потенциала для совершенных и разбавленных растворов:

и

определим хим. потенциал компонента в реальном растворе как:

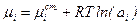
Таким образом, активность представляет собой такую величину, подстановкой которой в выражение для хим. потенциалов идеальных растворов вместо концентрации мы рассчитываем µ_i реального раствора. Следовательно, для совершенных и разбавленных растворов a_i совпадает с N_i и C_i.

Из уравнения следует, что при a_i=1 µ_i=µ_{i ст.}, где µ_{i ст} - химический потенциал компонента в стандартном состоянии (не путать со стандартными условиями). Т.о. в стандартном состоянии активность равна единице. Из сказанного видно, что термодинамическая активность вводится формально.

Другое определение активности, которое может быть выведено из предыдущего, если рассматривать газовую фазу как идеальную (что в большинстве случаев справедливо для металлургических процессов):

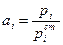
т.е. активность данного компонента в растворе, как отношение давления пара этого компонента над раствором к давлению его пара в стандартном состоянии. Активность пропорциональна давлению пара и характеризует тенденцию компонента покинуть данную фазу. Из уравнения следует, что активность безразмерная величина.

Уравнение сохраняется и при расчете систем с реальными газами (при высоких давлениях), с заменой парциальных давлений на летучесть (фугитивность) газа.

Выбор стандартного состояния

Для растворов разных типов удобно выбирать и различные стандартные состояния. Его необходимо выбирать так, чтобы в идеальных случаях активность совпадала с концентрацией и сохранялась бы форма записи основных уравнений для идеальных законов.

Для совершенных растворов:

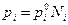или

Для растворов, близких к совершенным (т.е. в растворе рассматривается поведение всех компонентов во всем диапазоне составов) в качестве стандартного состояния принимается чистый компонент 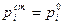. Тогда 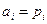/ . a_i для растворов, близких к совершенным, всегда меньше единицы и только для компонента, находящегося в чистом состоянии, активность равна единице.

Если поведение раствора отклоняется от совершенного, то a_i не равно N_i. Степень отклонения определяется величиной коэффициента активности (γ_i):

a_i/N_i=γ_i

В совершенных растворах γ_i=1. Для реальных растворов коэффициент активности может быть как больше единицы (положительные отклонения) так и меньше единицы (отрицательные отклонения). Для реальных растворов закон Рауля сохраняет свою форму при замене концентрации на активность:

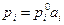
В случае разбавленных растворов для растворителя также как и для совершенных растворов необходимо, чтобы сохранялась форма записи закона Рауля, поэтому также как и для совершенных растворов в качестве стандартного состояния удобно принять чистое вещество. Тогда для растворителя закон Рауля запишется в виде уравнения.

Для растворенного вещества справедлив закон Генри. Поэтому в качестве стандартного состояния принимают такое состояние компонента, в котором 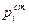=1/г_i. Тогда:

p_i = a_i∙ 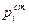_.= a_i/г_i

Форма записи закона Генри сохраняется при любых концентрациях при замене C_i на a_i. При рассмотрении таких растворов также вводят коэффициент активности, равный отношению a_i/C_i. В отличие от растворов, близких к совершенным, его принято обозначать f_i.

По одному из определений термодинамическая активность есть величина, подстановка которой вместо концентраций в термодинамические уравнения делает последние применимыми для реальных растворов (только уравнения, описывающие равновесие).

Закон действующих масс.

Возьмем реакцию:

A + 2C = 3D

Для разбавленных растворов закон действующих масс записывается:

K_c=C_D³/(C_А∙C_С²)=f(T)

Из условия равновесия (∆G=0 или 3µ_D=µ_A+2µ_C) при замене в термодинамических уравнениях концентрации на активность легко получается, что для реальных растворов:

K_A=a_D³/(a_A∙a_C²)=f(T)

т.е. и закон действующих масс применим для реальных растворов, если вместо концентраций используется активность.

Введение понятия термодинамической активности оказалось весьма эффективным и полезным для расчетов равновесий в реальных химических системах. В современной технической литературе данные по равновесиям излагаются преимущественно в терминах активности. Еще раз отметим, что понятие активности чисто формальное, однако измерения активности полезны не только для решения конкретных задач по равновесиям, но и для систематизации опытных данных, для развития теории растворов. По отклонению активности от идеальных растворов судят о тенденциях в характере межчастичных взаимодействий в растворах.

Методы определения активности. Экспериментальные методы определения активности основаны главным образом на изучении равновесий между реальными растворами и другими фазами, в которых активность компонента известна. Такими фазами могут быть смеси идеальных газов, разбавленные или совершенные растворы, а также другие фазы, в которых активность определена независимым путем или описывается простыми законами. Могут быть использованы и чистые в-ва или в-ва в другом стандартном состоянии, активность которых равна единице.

Измерение давления пара. Этот способ удобен для летучих компонентов. Основанные на его использовании расчеты непосредственно вытекают из уравнения для определения активности и достаточно просты. Однако измерение давления пара, особенно в системах, представляющих интерес для металлургии, в ряде случаев связаны со значительными трудностями (малые значения парциальных давлений, взаимодействие расплавов с материалом тиглей при высоких температурах).

Для близких к совершенным растворов активность компонента в растворе определяется из измерений давления его пара над раствором и в чистом состоянии: a_i=p_i/ . Например, давление пара жидкого цинка при 957 К =0,0612 атм., а его давление над сплавом Zn-Sn, при N_Zn=0.226, составляет p_Zn=0,0208 атм. Отсюда:

a_Zn=0,0208/0,0612=0,34 и γ_Zn=0,43/0,226=1,505

Для разбавленных растворов активность растворителя определяется также, а активность растворенного в-ва из уравнения a₂=г₂∙p₂. Для определения г₂ - в области больших разведений, где C₂/p₂=пост., кас. в области к кривой p от C при C-->0.

Изучение хим. равновесия. Активности малолетучих компонентов, например углерода, практически невозможно определить из измерений давления пара. В таких случаях используют изучение хим. реакции, в которой участвует этот компонент и образуется газообразный продукт. Так, для раствора углерод в γ-Fe (аустенит) можно воспользоваться реакцией:

[C] + 2H₂ = CH₄

константа равновесия которой K=p_CH4/(p_H2²∙a_C). Для нахождения K необходимо определить соотношения p_CH4/(p_H2²∙[C]) при низких концентрациях углерода, при которых активность углерода равна его концентрации, и экстраполировать эти значения на нулевую концентрацию C.

Активность закиси железа в жидком шлаке может быть найдена, например, путем изучения равновесия :

[FeO] +CO_(г) = [Fe] +CO_2(г)

где K находится по составу газовой смеси, равновесной с чистым железом (a_Fe=1).

Для определения активностей используют также метод измерения электродвижущих сил гальванических элементов.