Понятие о многомассовой системе электропривода.

Многомассовая система рассматривается как 2-х массовая. И в этом случае рассматривается влияние упругости и зазоров в механических звеньях на движение электропривода.

Рассчитываем влияние упругости на следующем примере. Пусть механическая часть электропривода включает в себя один невесомый упругий элемент с коэффициентом жесткости С₀ и зазором d₀. Все остальные элементы принимаем абсолютно жесткими и без зазоров, тогда приведенный к валу двигателя зазор и коэффициент жесткости имеет следующий вид:

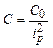- для вращающего движения,

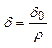- зазор для элемента с постоянным движением,

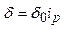- зазор для элемента с вращающимся движением,

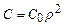- постоянное движение.

Остальные элементы (массу, крутящий момент, инерционность) приводят к валу двигателя по обычным формулам.

В результате все маховые массы привода сводятся к 2-м, одна их которых жестко связана с двигателем и обладает моментом инерции J₁, а другая - длина двигателя с зазором и упругим элементом и обладает моментом инерции J₂.

Такую 2-х массовую систему можно представить в виде следующего рисунка

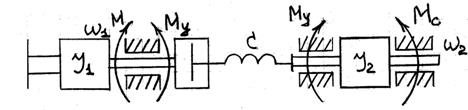
Модель многомассовой системы электропривода представляет собой систему электропривода, где из-за наличия упругих элементов или зазоров законы движения отдельных элементов привода не совпадают во времени. Если для данной системы модели затормозит второй вал, то возможно вращение первого вала в пределах, определенных диапазоном упругой деформации элемента «с», если затормозит первый вал, то возможно с учетом указанных ограничений движение вращения второго вала. Таким образом в отличие от одномассовой жесткой механической системы двухмассовая система обладает двумя степенями подвижности. Для математического описания движения такой модели электропривода упругий элемент мысленно разрезают, а маховым массам первой и второй прикладывают равный и противоположно направленный элемент Му в упругом элементе. Тогда движение двухмассовой системы можно описать следующей системой уравнений:

; ;

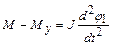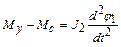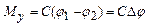
j₁, j₂ – углы поворота на концах упругих звеньев

; ;

;

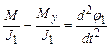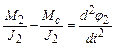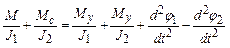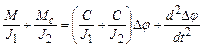; М_у=СDj;

;

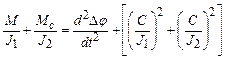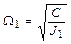- угловая частота свободных колебаний первой маховой массы,

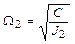- угловая частота свободных колебаний второй маховой массы.

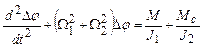- уравнение характеризует систему как консервативную, в которой при внешнем возмущении возникает незатухающие гармонические колебания с угловой частотой .

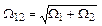Если внешнее возмущение будет действовать на механическую часть с той же частотой, то может возникнуть резонанс.

В реальном электроприводе всегда имеем потери на сухое и вязкое трение и такое упругое звено не может быть консервативным.

Сухое трение деформирует такие колебания, в которых скорость изменяет свой знак.

Вязкое трение всегда оказывает деформирующее трение. Это трение возникает при работе вращающих элементов в жидкой или воздушной среде.

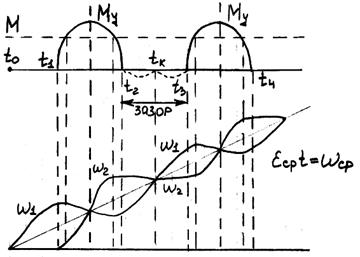
Есть двухмассовая система электропривода с зазором. Движение отдельных масс происходит следующим образом: в начале, когда зазор не выбран, движется масса J₁ под воздействием момента М и, как только выбирается зазор (момент времени t_1,) появляется момент упругой силы - первая масса тормозится, начинается разгон второй массы (точка t_1), в точке t₂ вновь начинается разгон первой массы. Вторая масса из точки t₃ движется с постоянной скоростью, разгон первой массы происходит линейно, в точке t₄ выбирается зазор первая масса тормозится, начинает появляться упругий момент и разгоняется вторая масса и т.д.

Колебания системы затухают, в виду наличия сухого и вязкого трения, и механическое звено будет двигаться с неизменной скоростью и при постоянном моменте упругих сил.