Предмет и задачи строительной механики

Строительной механикой в широком смысле называется наука о методах расчета сооружений на прочность, жесткость и устойчивость. К ней относятся следующие дисциплины: сопротивление материалов, строительная механика стержневых систем, строительная механика пластин и оболочек, теория упругости, теория пластичности и теория ползучести.

Сопротивление материалов рассматривает вопросы прочности, жесткости и устойчивости отдельных элементов сооружения.

Строительная механика (или теория сооружений) занимается расчетом сложных конструктивных форм и сооружений в целом.

Строительная механика делится на разделы:

а) статика сооружений, изучающая расчеты на прочность при действии статической нагрузки (в том числе и подвижной);

б) динамика сооружений;

в) теория устойчивости сооружений.

Теория упругости, теория пластичности и теория ползучести решают те же задачи расчета сооружений, но в более строгой постановке, т.е. не учитывая некоторые упрощающие допущения, принятые в строительной механике и сопромате.

При этом в курсе теории упругости изучаются случаи, когда в сооружении возникают только упругие деформации, а в курсе теории пластичности – когда возникают и пластические деформации.

В своих решениях строительная механика пользуется методами теоретической механики, графической статики, сопротивления материалов, теории упругости и теории пластичности.

Строительная механика в начальный период развития не была самостоятельной наукой, а сливалась с общей механикой.

Как самостоятельная наука строительная механика стала успешно развиваться лишь в первой половине ХIX в. в связи с начавшимся усиленным строительством мостов, железных дорого, плотин, судов и крупных промышленных сооружений.

Строительная механика является наукой экспериментально-теоретической, т.к. базируется на результатах испытаний сооружений (в натуре и на моделях), опыте их эксплуатации и теоретических исследованиях.

Сложность строгого учета взаимодействия отдельных частей сооружения, всех факторов, влияющих на его поведение, вызывает необходимость рассматривать при расчете не действительное сооружение, а упрощенную схему его, называемую расчетной схемой сооружения.

Расчетные схемы сооружений

Расчетная схема – это упрощенное изображение действительной схемы сооружения. При выборе расчетной схемы следует руководствоваться двумя основными требованиями:

– схема должна возможно более соответствовать действительным условиям работы сооружения;

– схема должна быть возможно более простой, чтобы избежать излишней сложности при расчете.

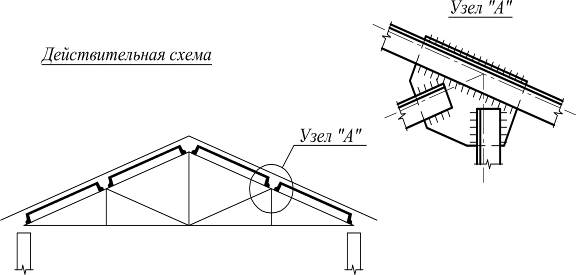
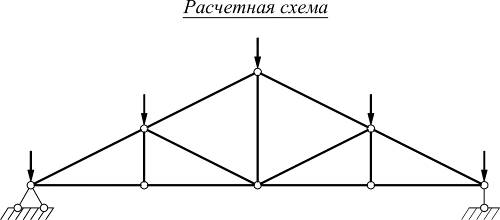
Классификация расчетных схем сооружений.

I. По геометрическим признакам:

а) стержневые системы – сооружения, составленные из элементов, поперечные размеры которых значительно меньше их длин;

б) пластинки и оболочки – сооружения, составленные из элементов, толщина которых относительно мала по сравнению с шириной и длиной;

в) массивные сооружения, у которых все три размера соизмеримы.

II. В зависимости от типа соединений элементов:

а) системы с жесткими соединениями элементов – рамы;

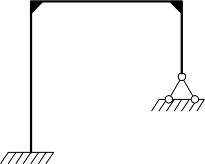
б) системы с шарнирными соединениями элементов в узлах;

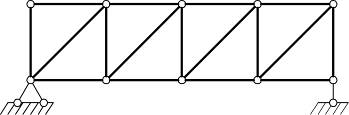
в) с комбинированным соединением.

III. По направлению опорных реакций:

а) безраспорные системы – в которых вертикальная нагрузка вызывает только вертикальные опорные реакции;

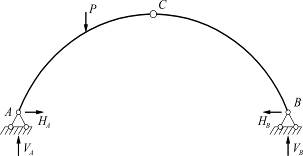
б) распорные системы – в которых от вертикальной нагрузки возникают вертикальные и горизонтальные опорные реакции.

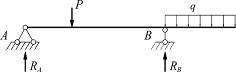
а) безраспорные системы	б) распорные системы

Классификация опор:

а) шарнирно-подвижная опора;

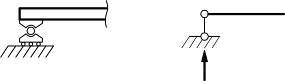
Соп=1

б) шарнирно-неподвижная опора;

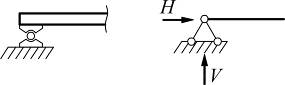
Соп=2

в) жесткое защемление;

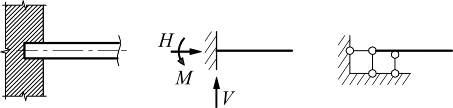
Соп=3

Кинематический анализ сооружений

Расчетные схемы сооружений могут быть представлены в виде системы геометрически неизменяемых тел, соединенных между собой шарнирами и прикрепленных к земле при помощи опорных устройств.

Эти шарниры и опоры называются кинематическими связями или просто связями, а геометрически неизменяемые тела – дисками.

Геометрически неизменяемой называется такая система соединенных между собой тел, которая не допускает относительного перемещения ее частей без их деформаций.

Для уяснения сущности кинематического анализа систем, предварительно рассмотрим отдельный, ничем не связанный плоский диск.

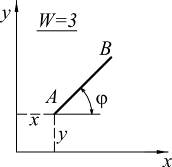
Степенью свободы (W) называется количество независимых геометрических параметров, определяющих положение конструкции в пространстве или на плоскости.

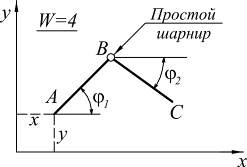
Простой шарнир уменьшает степень свободы на

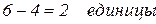
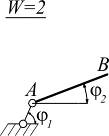
Опорный стержень уменьшает степень свободы на

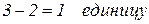
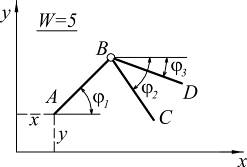
Шарнир, соединяющий три диска, эквивалентен двум простым шарнирам

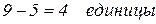
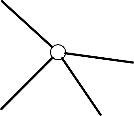
Если шарнир соединяет n стержней, то он эквивалентен n-1 простым шарнирам.

Тогда степень свободы системы в целом определится:

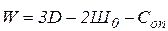
где D – число дисков; Ш_о – число простых шарниров; С_оn – количество опорных связей.

Если:

W = 0 – система геометрически неизменяема и статически определима;

W > 0 – система геометрически изменяема;

W <0 – система геометрически неизменяема и статически неопределима.

Условие W < 0 является необходимым, но недостаточным условием геометрической неизменяемости системы. Следует еще рассмотреть расположение стержней и шарниров, т.е. проверить структуру системы.

Мгновенно изменяемые системы

Примерами мгновенно изменяемых систем могут являться:

1. Системы, в которых три шарнира лежат на одной прямой

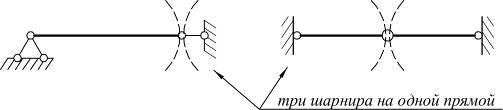
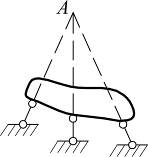
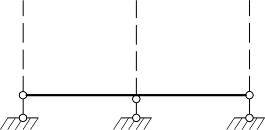
2. Системы, в которых линии действия опорных реакций пересекаются в одной точке либо пересекаются в бесконечности (параллельны)

а) линии действия опорных реакций пересекаются в одной точке	б) линии действия опорных реакций пересекаются в бесконечности (параллельны)

Примеры: определить степень свободы и провести структурный анализ сооружений:

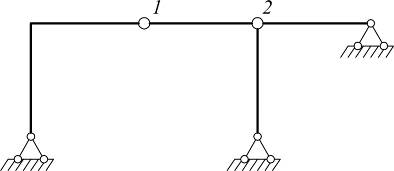
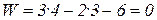система статически определима и геометрически неизменяема

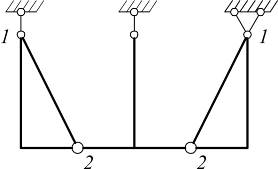
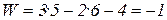система статически неопределима и геометрически неизменяема

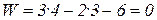система статически определима, но мгновенно изменяемая