Лекция 6. Расчет статически определимых плоских ферм

При расчете плоских статически определимых ферм используются основные уравнения статики твердого тела. Причем, до начала расчета необходимо определить опорные реакции.

В основу определения усилий в стержнях фермы положен известный из сопромата метод сечений. Для определения внутренних усилий следует выделять сечениями узлы или отдельные части фермы и рассматривать условия их равновесия под действием внешних нагрузок и усилий в расчетных стержнях.

Уравнения следует составлять таким образом, чтобы усилия в элементах фермы определялись наиболее просто, без совместного решения системы уравнений. Это позволяет не только значительно упростить расчет, но и получить более точные результаты.

Существует несколько аналитических способа расчета ферм:

Способ вырезания узлов

При определении усилий в стержнях ферм способом вырезания узлов, приходится иметь дело с плоской системой сходящихся сил.

Сущность способа состоит в следующем: поскольку вся ферма находится в равновесии, то и любой ее узел должен находиться в равновесии.

Т. к. для плоской системы сходящихся сил можно составить только два независимых уравнения ∑F_x = 0 и ∑F_y = 0, то расчет фермы следует начинать с двухстержневого узла и далее вырезать узлы, в которых сходится не более 2-х стержней с неизвестными усилиями.

Способ вырезания узлов применяется для наиболее простых ферм. Усилия в стержнях приходится определять через ранее найденные усилия, а это проводит к накоплению и увеличению ошибок в расчетах.

Рассмотрим пример расчета фермы методом вырезания узлов:

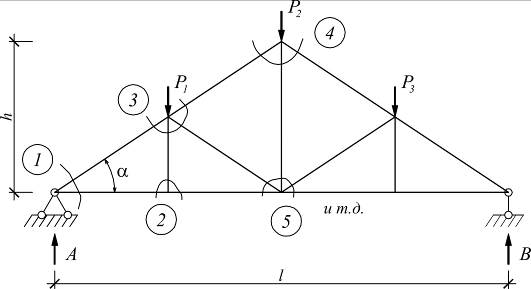
1)

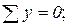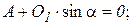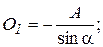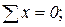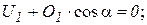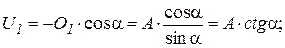
2)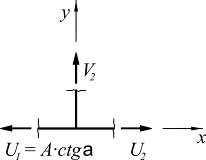

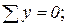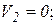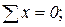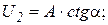
Частные случаи способа вырезания узлов:

1. Если в узле сходится два стержня и больше никаких сил к этому узлу не приложено, то усилия в обоих стержнях = 0.

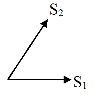
∑Y = 0; => S2 = 0; ∑X = 0 => S1 = 0;

2. Если к двухстержневому узлу приложена сила, направленная вдоль одного из них, то усилие в этом стержне равно силе по величине, но противоположно направлению, а во втором стержне усилия=0.

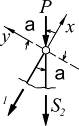
∑Y = 0 => S1 = -p; ∑X = 0 => S2 = 0;

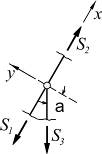
∑X = 0; => S1 = S2; ∑Y = 0 => S3 = 0;

3. Если в узле сходятся три стержня, из которых два направлены вдоль одной прямой, то усилия в третьем стержне равно нулю, а в первых двух равны между собой.

4. Если в узле сходятся три стержня, из которых два направлены вдоль одной прямой и есть нагрузка, направленная по оси третьего стержня, то усилия в этом стержне равно силе по величине, но противоположно направлено, а усилия в двух первых стержнях равны между собой.

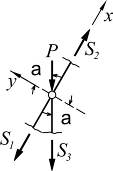
∑X = 0; => S1 = S2; ∑Y = 0 => S3 = -p;

5. В четырехстержневом узле, где стержни попарно направлены вдоль одной прямой, усилия также которого равны между собой.

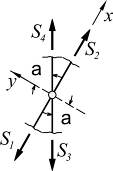
∑X = 0 => S3 = S4. ∑Y = 0; => S1 = S2;

Способ моментной точки

Способ моментной точки применяется в тех случаях, когда ферму можно рассечь на две части так, чтобы при этом перерезанными оказались три ее стержня, направления осей которых, не пересекаются в одной точке.

Сущность метода заключается в следующем: проводят сечения, через три стержня, и составляют уравнения равновесия одной из частей фермы относительно так называемой моментной точки. Моментной точкой для рассматриваемого стержня называется точка пересечения двух других рассеченных стержней.

Отбрасываем одну из частей фермы (проще левую) и рассматриваем в равновесии правую отсеченную часть фермы. Моментные точки для стержней S₁, S₂, S₃ соответствует 1, 2, 3.

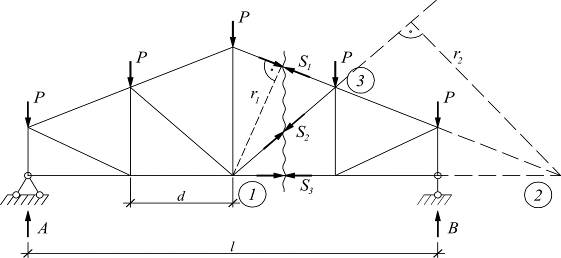
Чтобы определить S₁:

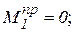
и т.д.

Способ проекций

Это способ применяется в случае, когда два из трех рассеченных стержней параллельны между собой.

Как и в способе моментных точек, проводится сечение через три стержня и рассматривается в равновесии одна из отсеченных частей фермы.

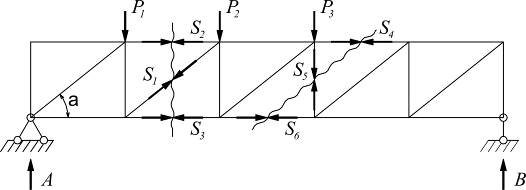
Уравнение моментов для определения усилия S₁ составить невозможно, т.к. моментная точка находится в бесконечности. Поэтому, рассматривая в равновесии, допустим левую часть фермы, составляют уравнение суммы проекций всех сил на ось у.

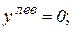
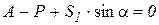
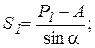и т.д.

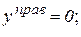
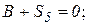
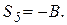
Способ моментных точек и способ проекций обладают тем преимуществом, что позволяют определять усилия в отдельно взятых стержнях, не зависимо от других усилий, что уменьшает величину ошибок.