Лекция 10. Расчет статически неопределимых систем методом сил. Статически неопределимые системы и их свойства
Статически неопределимыми называются системы, которые не могут быть рассчитаны с использованием только условий равновесия. Для их расчета необходимо составлять дополнительные уравнения, характеризующие деформацию данной системы.
В статически неопределимых системах имеются так называемые лишние связи, т. е. связи, которые необходимо удалить из статически неопределимой системы, чтобы получить систему статически определимую и геометрически неизменяемую.
Статически неопределимые системы экономичнее статически определимых. Недостатком статически неопределимых систем является их чувствительность к осадкам опор, к температурным воздействиям и неточности изготовления отдельных элементов системы.
Например, простая балка при осадке опор займет новое положение, оставаясь прямолинейной и не испытывая никаких добавочных напряжений, в статически неопределимой неразрезной балке, осадка опоры будет сопровождаться искривлением оси балки и появлением добавочных напряжений.
| а) |
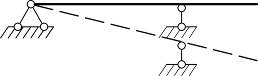
| |
| б) |
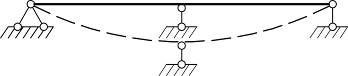
| |
| в) чувствительность к перепаду температур |
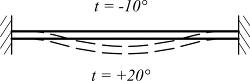
| |
Степень статической неопределимости
Степень статической неопределимости определяется количеством лишних связей системы.
Количество лишних связей системы:
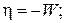
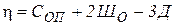
|
Здесь Соn – число опорных связей;
Шо – число простых шарниров;
Д – число дисков в системе.
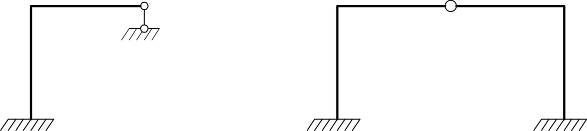
| |
 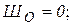 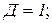
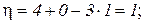
| 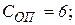 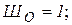 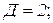
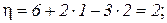
|
Если рама состоит из К замкнутых контуров, имеющих шарниры, то статической неопределимости такой рамы необходимо определять.
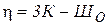
|
Здесь К – число замкнутых контуров;
Шо – число простых шарниров.
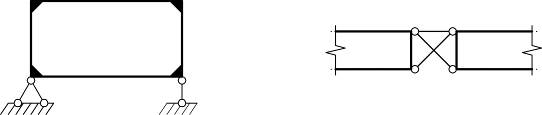
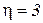
Замкнутый контур трижды статически неопределим, а простой шарнир уменьшает кол-во связей на единицу.
Основная система метода сил
Основной называется система, которая получается из заданной статически неопределимой системы путем отбрасывания лишних опорных или внутренних связей. Основная система должна быть статически определимой и геометрически неизменяемой.
Способы образования:
1.Можно отбросить лишние опорные связи и по направлению каждой отброшенной связи приложить соответствующую неизвестную реакцию;
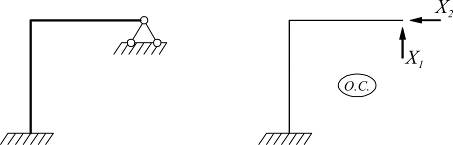
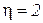
2.Можно разрезать сплошной брус, в сечении приложить опорные моменты, поперечные и продольные силы;
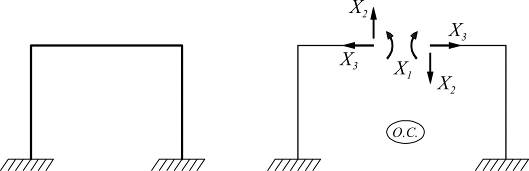
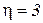
3.Можно удалять одну внутреннюю связь, путем введения на ось жесткого шарнира. По обе стороны от шарнира следует прикладывать парные моменты;
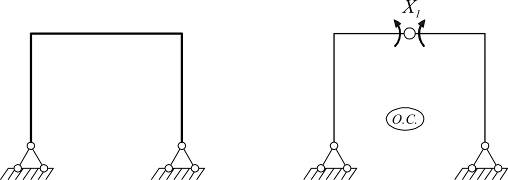
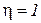
4.Можно сделать разрез по шарниру, это равносильно удалению двух связей. По обе стороны разреза прикладывают парные поперечные и продольные силы.
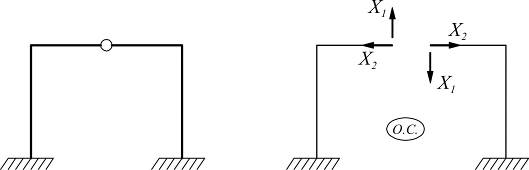
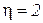
5.Можно разрезать стержень с шарнирным закреплением концов, при этом прикладываются только продольные силы, т.к. такой стержень работает только на сжатие или растяжение.
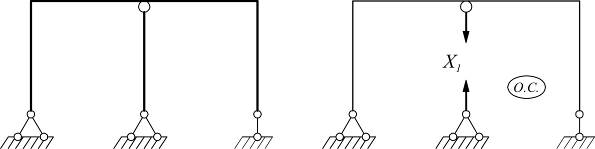
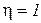
Примечание: необходимо различать связи абсолютно необходимые и условно необходимые. Абсолютно необходимые – это связи, при удалении которых система становится геометрически изменяемой.
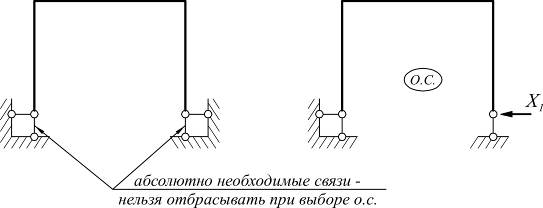
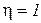
Пример образования основной системы:
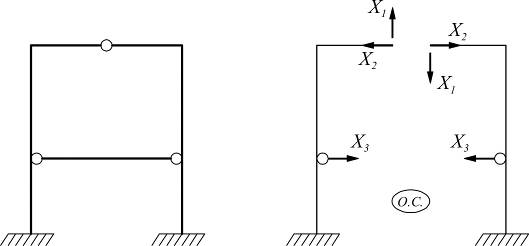
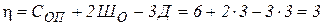
Канонические уравнения метода сил
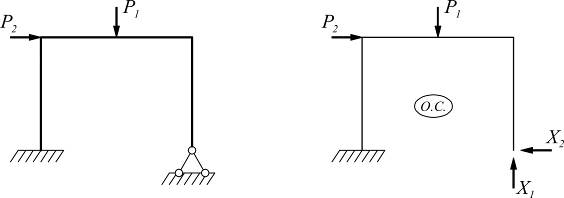
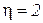
В заданной системе перемещения по направлению отброшенных связей (горизонтальное и вертикальное) равны нулю. В основной системе эти же перемещения могут быть как = 0 так и ≠ 0.
Для того, чтобы заданная система и основная были равноценны в смысле перемещений и усилий, необходимо, чтобы перемещение по направлению отброшенных связей в основной системе, от действия внешней нагрузки и реакций отброшенных связей были = 0.
Т.е., для рассматриваемого случая:
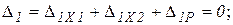
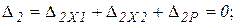
Если обозначить 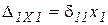 , а
, а 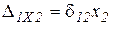 и т.д., то система канонических ур-ний запишется:
и т.д., то система канонических ур-ний запишется:

здесь 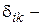 переменная по направлению i от действия хк=1;
переменная по направлению i от действия хк=1;
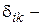 переменная по направлению i от действия внешней нагрузки;
переменная по направлению i от действия внешней нагрузки;
Определяют перемещения по интегралу Мора, учитывая влияние на перемещение только изгибающих моментов, т. е.:
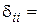
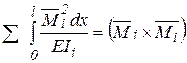
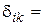
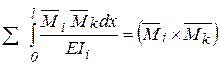
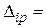
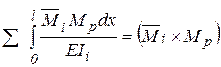
Дата добавления: 2016-02-04; просмотров: 3614;
