Лекция 9. Арки с затяжками
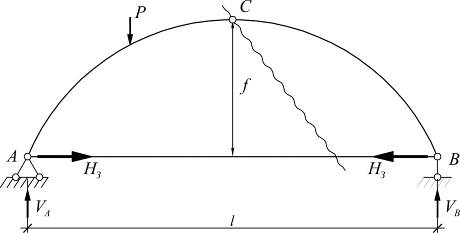
Арка с затяжкой в отношении опорных реакций является балочной системой: от вертикальной нагрузки возникают только вертикальные опорные реакции Va и Vb, которые определяются так же как в простой балке.
∑Ma = 0 => Vb; ∑Mb = 0 =>Va
Чтобы определить внутренние усилия в сечениях арки M, Q, W, необходимо вначале определить усилия в затяжке Нз. Для этого проводим сечение через ключевой шарнир С и затяжку. Приравнивая сумму моментов левых или правых сил относительно шарнира С к нулю, определяем Нз.
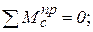
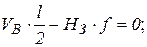
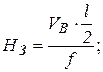
Внутренние усилия в сечения арки с затяжкой определяются аналогично трехшарнирной арке.
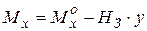
|

|
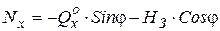
|
Арка с повышенной затяжкой
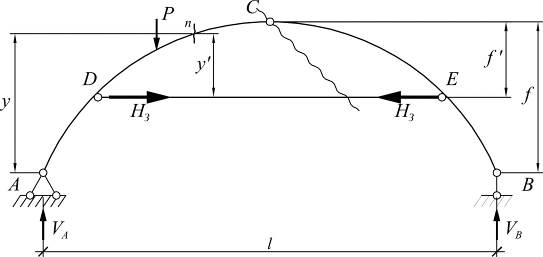
Опорные реакции Vа, Vв и усилия в затяжке Нз определяются как в предыдущем случае:
∑Mа = 0 => Vв; ∑Mв = 0 => Vа; ∑Mс = 0 => Нз
Внутренние усилия в поперечных сечениях арки определяются:
1) на участке ДСЕ:
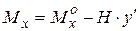 ;
;
 ;
; 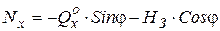 ;
;
2) на участках АД и ВЕ:
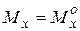 ;
; 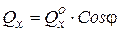 ;
; 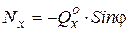 ;
;
Теория перемещений. Определение перемещений по формуле (интегралу) Максвелла-Мора
Перемещение любых упругих систем могут определятся по формуле (интегралу) Максвелла-Мора, которая при учете только силовых воздействий, имеет вид:

| (1) |
Интегрирование ведется по участкам, в интеграле Мора принято обозначение:
Мр, Qр, Wр – аналитическое выражение изгибающего момента поперечной и продольной силы на рассматриваемом участке от действия заданной внешней нагрузки;
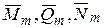 – выражение изгибающего момента, поперечной и продольной силы на рассматриваемом участке от действия единичной обобщенной силы действующей по направлению искомого перемещения;
– выражение изгибающего момента, поперечной и продольной силы на рассматриваемом участке от действия единичной обобщенной силы действующей по направлению искомого перемещения;
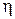 – коэффициент, учитывающий неравномерность распределения касательных напряжений по сечению;
– коэффициент, учитывающий неравномерность распределения касательных напряжений по сечению;
EI, GF, EF – соответственно жесткость элементов при изгибе, сдвиге и растяжении (сжатии)
При определении перемещений балок и рам, где главную роль играют деформации изгибе, учитывают только первый член интеграла Мора. Второе и третье слагаемые формулы Мора не учитывают, т. к перемещение вызванные сдвигом и растяжением (сжатием) элементов составляют около
3–5 % от полной их величины
Пример.
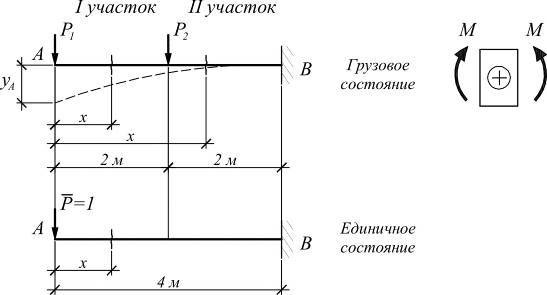
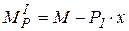 ; ;
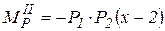 ; ;
| 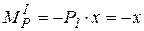 ; ;
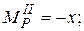
|
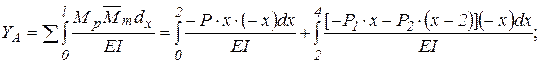
Для упрощения вычислений интеграла Мора используется правило Верещагина, позволяющее заменить интегрирование аналитических выражений перемножением эпюр. Правило Верещагина можно использовать для прямолинейных элементов постоянной жесткости.
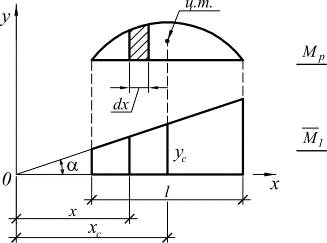
| |
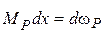 ; ;
| 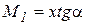
|
тогда: 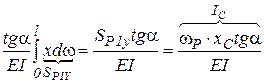 ;
;
где:
 статический момент площади грузовой эпюры относительно оси у.
статический момент площади грузовой эпюры относительно оси у.
т.е. 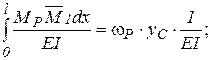
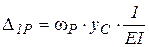
|
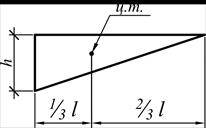
Результат перемножения двух опор равен произведению площади одной опоры на ординату взятую из другой (прямоугольной опоры) под у. т. первый
Порядок расчета по правилу Верещагина:
1. Строится грузовая эпюра.
2. По направлению искомого перемещения прикладываются ед. усилие: Р = 1 – если отыскивается линейное перемещение и М = 1 – если необходимо определить угол поворота сечения.
3. Строится эпюра единичного момента.
4. По правилу Верещагина перемножаются единичные эпюры на грузовую. Если перемножаемые эпюры расположены по одну сторону элемента, то результат перемножения (+), если по разные (–).
5. Перемножение эпюр ведут по участкам, границами участков являются узлы рам, точки приложения сосредоточенных усилий, точки начала и окончания приложения распределенной нагрузки, точки изменения жесткости элементов.
6. Если результат перемножения эпюр получаем со знаком (–), то это значит, что направление перемещения противоположно направлению единичной силы
Примечание: по правилу Верещагина можно перемножать эпюры, когда одна из них прямолинейна; площадь эпюры можно брать из любой эпюры, ординату – только из прямолинейной.
| Эпюра | Площадь |
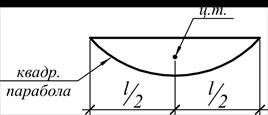
| 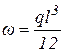
|
| 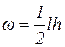
|
Пример.

|
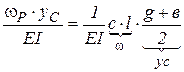
|
Дата добавления: 2016-02-04; просмотров: 5625;
