Синусоидальных величин.
Ток, величина которого изменяется во времени по синусоидальному закону и значения которого повторяются через равные промежутки времени, называется переменным синусоидальным током. Он характеризуется периодом, амплитудой, мгновенным значением и фазой. Полный круг изменения синусоидального тока называется циклом, а время одного цикла называется периодом. Длительность периода обозначается символом «Т». Величина обратная периоду называется частотой, она имеет размерность «с-1», Герц.
f = s w:val="36"/></w:rPr><m:t>1</m:t></m:r></m:num><m:den><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="36"/><w:sz-cs w:val="36"/><w:lang w:val="EN-US"/></w:rPr><m:t>T</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  .
.
Значение синусоидального тока в данный момент времени называется мгновенным. Мгновенное значение обозначается символом «i». Синусоидальные токи возникают в цепях под действием синусоидальных ЭДС и напряжений, мгновенные значения которых обозначаются символами «e» и «u». Максимальные значения синусоидальных токов напряжений и ЭДС обозначаются символами «Im», «Um» и «Em» и называются амплитудными.
В практике инженерных расчетов удобнее пользоваться не мгновенными и амплитудными значениями синусоидальных величин, а действующими.
Действующее значение синусоидального тока численно равно такому значению постоянного тока, который за время одного периода синусоидального тока выделяет в элементе цепи такое же количество теплоты, что и синусоидальный ток.
Действующие значения синусоидальных электротехнических величин обозначаются символами «I», «U», «Е», они меньше амплитудных в 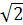 раз.
раз.
U= 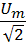 , I=
, I= 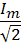 .
.
Фаза характеризует численное значение и знак синусоидальной величины в данный момент времени, а начальная фаза значение синусоидальной величины и знак в начальный момент времени. Фаза измеряется в угловых единицах или в долях периода.
Любую синусоидальную величину можно описать аналитически, графически, и вращающимся вектором. Аналитическое описание дает уравнение зависимости мгновенного значения синусоидальной величины от времени.
i=ImSin(ωt+ψ),
где ωt-фаза, а ω-угловая частота. В промышленных сетях большинства стран ω=314 рад/с.
t-время.
ψ-начальная фаза.
Графическое описание, это зависимость мгновенного значения синусоидальной величины от времени, построенная в прямоугольной системе координат.
| Im |
| T |
| t |
| i |
| (a) |
| (б) |
| Im |
| i |
| φ=ωt |
| ψ=0 |
| ω=const |
Рис.2.1. Изображение синусоидального тока в прямоугольной системе
координат (a) и вращающимся вектором (б)
| Im2 |
| Im1 |
| Im3 |
| 2 А |
| ψ |
Рис. 2.2 Векторное сложение синусоидальных токов.
При изображении синусоидальной величины вращающимся вектором его длина является амплитудой синусоиды, угол между вектором и положительным направлением горизонтальной оси фазой синусоидальной величины. Скорость вращения вектора есть угловая частота, а его проекция на вертикальную ось мгновенное значение.Система векторов вместе с осями координат называется векторной диаграммой. Векторная диаграмма позволяет свести электротехническую задачу к задаче геометрической, к расчету треугольников. Например, к узлу А цепи подходят токи i1=10Sin314t, и i2=5Sin(314t+  ). Необходимо найти закон изменения тока i3, уходящего от узла.
). Необходимо найти закон изменения тока i3, уходящего от узла.
Построение диаграммы начинают с выбора масштаба. Пусть в одном масштабном отрезке будет 2 А. В момент времени t=0 проекция вектора 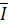 1 на вертикальную ось i1=10Sin0=0, следовательно, располагается он вдоль горизонтальной оси и имеет длину 5 масштабных отрезков, проекция вектора
1 на вертикальную ось i1=10Sin0=0, следовательно, располагается он вдоль горизонтальной оси и имеет длину 5 масштабных отрезков, проекция вектора 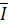 2 в этот же момент времени i2=5Sin
2 в этот же момент времени i2=5Sin 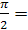 5, т.е располагается он вдоль вертикальной оси и имеет длину 2,5 масштабных отрезка. Для нахождения амплитуды тока i3 необходимо сложить по правилу параллелограмма векторы
5, т.е располагается он вдоль вертикальной оси и имеет длину 2,5 масштабных отрезка. Для нахождения амплитуды тока i3 необходимо сложить по правилу параллелограмма векторы 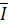 1 и
1 и 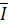 2, а для нахождения его длины необходимо воспользоваться теоремой Пифагора.
2, а для нахождения его длины необходимо воспользоваться теоремой Пифагора.
I3= 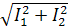 =
= 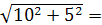 11,18.
11,18.
Начальная фаза тока i3 находится по тангенсу угла, образованного вектором 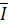 3 и горизонтальной осью.
3 и горизонтальной осью.
ψ = arctg 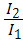 = arctg
= arctg 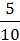 =26,560.
=26,560.
Закон изменения тока, уходящего от узла:
i3=11,18Sin(314t+26,56).
Геометрическое сложение векторов может быть заменено на аналитическое, при их описании комплексными числами. Положение вращающегося вектора на плоскости можно обозначить двумя способами:
● задавая его проекции на оси координат;
● задавая его длину (в математике длина вектора называется модулем) и угол, который вектор образует с положительным направлением горизонтальной оси.
| b |
| a |
| A |
| +j |
| -j |
| +1 |
| -1 |
| φ |
Рис. 2.3. Вращающийся вектор
на комплексной плоскости
На комплексной плоскости горизонтальная ось обозначается символами «+1» и «-1» и называется осью действительных величин. Вертикальная ось -символами «+j» и «-j» и называется осью мнимых величин. j= 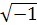 и называется мнимой единицей.
и называется мнимой единицей.
Положение вектора на комплексной плоскости рис.2.3 можно записать:
A=a+jb.
Сомножители 1 перед a и j перед b указывают, на какие оси спроектирован вектор. Подчеркивание снизу символа А означает комплексную величину.
Такая форма записи называется алгебраической, она удобна при проведении операций сложения и вычитания. Например, требуется сложить два вектора: А= 10+j3 и B=15-j7.
А+ B=10+j3+15-j7=25-j4.
Из рис.2.3 видно, что проекции вектора А на оси равны:
a=ACosφ, b=ASinφ,
где А – модуль или длина вектора А (обратите внимание, что этот символ не имеет никаких подчеркиваний).
Тогда:
А= ACosφ+jASinφ=А(Cosφ+jSinφ).
Такая форма записи комплексного числа называется тригонометрической. Учитывая, что Cosφ+jSinφ= 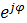 , получаем:
, получаем:
А=А 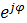 .
.
Полученная форма записи комплексного числа называется показательной, она удобна для умножения и деления. Например, требуется перемножить и разделить векторы: А=5 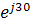 , B=10
, B=10 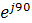 .
.
A×B=5 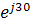 ×10
×10 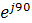 =
= 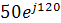 ,
,
 =
= 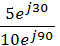 = 0,5
= 0,5  .
.
Для перехода от показательной формы записи к алгебраической и наоборот воспользуемся треугольником, выделенным на рис.2.3. Применяя теорему Пифагора, получим:
A=A 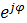 = ACosφ+ jASinφ=a+jb=
= ACosφ+ jASinφ=a+jb= 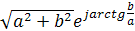 =A
=A 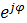 .
.
Например,
A=18 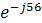 =18Cos(-56)+j18Sin(-56)=10-j15,
=18Cos(-56)+j18Sin(-56)=10-j15,
A=10-j15= 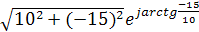 =18
=18 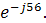
Метод расчета цепей с применением комплексных чисел называется символическим. При его использовании могут применяться все способы и формулы, применяющиеся при расчете цепей постоянного тока.
При дальнейшем изложении аналитическая форма описания синусоидальных токов и напряжений будет дублироваться комплексной.
Дата добавления: 2016-02-04; просмотров: 1548;
