Комплекс напряжения на зажимах цепи равен сумме комплексов напряжений на участках цепи.
После подстановки будем иметь:
U = 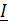 [R+j(XL-XC)] . (2.6)
[R+j(XL-XC)] . (2.6)
Выражение в квадратных скобках называется комплексом полного сопротивления, обозначается символом Z.
Z=[R+j(XL-XC)]=  (2.7)
(2.7)
где z= 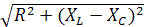 - модуль комплекса полного сопротивления;
- модуль комплекса полного сопротивления;
φ= 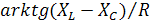 -угол сдвига фаз между током и напряжением.
-угол сдвига фаз между током и напряжением.
Подставляя в 2.4 комплекс действующего значения тока и комплекс полного сопротивления, получим:
U =I 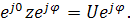 (2.8)
(2.8)
Вектор напряжения на зажимах последовательной цепи сдвинут относительно вектора тока на некоторый угол φ, знак и величина которого определяются параметрами цепи.
Из 2.8 и 2.6 вытекает закон Ома для действующих значений тока и напряжения и в комплексной форме:
I= 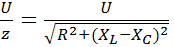 и
и 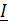 =
= 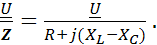 (2.9)
(2.9)
На основании уравнений2.3, 2.4 строится векторная диаграмма напряжений и тока. Начальная фаза тока равна нулю, поэтому вектор тока направлен вдоль положительного направления оси действительных величин. Векторы напряжений строятся в соответствии с уравнениями (2.4).
В одной фазе с вектором тока откладывается вектор напряжения на резисторе, модуль которого UR=I∙R. Вектор реактивного индуктивного напряжения,
модуль которого UL=I∙XL, опережает вектор тока на угол π/2 и откладывается вдоль положительного направления оси мнимых величин +j. Вектор реактивного емкостного напряжения, модуль которого UC=I∙XС, отстает от вектора тока на угол π/2, поэтому откладывается вдоль отрицательного направления оси мнимых величин –j. Вектор напряжения, подведенного на вход цепи, находится сложением построенных векторов по правилам векторной алгебры в соответствии с уравнением (2.5).

Рис. 2.5. Векторная диаграмма напряжений и тока
Действующее значение этого напряжения можно определить из заштрихованного треугольника, который называется треугольником напряжений:
U= 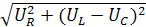 . (2.10)
. (2.10)
Из треугольника напряжений следует:
Ua=UR=UCosφ, Uр=UL-UC=Usinφ. (2.11)
Аналогичные соотношения для сопротивлений получаются из треугольника сопротивлений, который образуется путем деления всех сторон треугольника напряжений на ток.
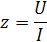
|
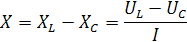
|
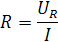
|
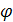
|
Рис. 2.6. Треугольник сопротивлений
Из треугольника сопротивлений следует:
R=z Cosφ, 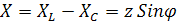 . (2.12)
. (2.12)
Дата добавления: 2016-02-04; просмотров: 1359;
