Особенности цепей с синусоидальными токами
Работа устройств переменного тока сопровождается возникновением переменного магнитного поля, вихревого электрического поля и явлениями самоиндукции. Под действием переменного магнитного поля сердечники электротехнических устройств перемагничиваются, а протекание переменного тока в проводниках сопровождается возникновением поверхностного эффекта. Под влиянием вихревого электрического поля в сердечниках возникают вихревые токи. Все эти явления вызывают дополнительные затраты мощности и приводят к кажущемуся увеличению сопротивления по сравнению с электротехническими устройствами постоянного тока.
R= 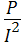 .
.
Поэтому при переменном токе параметр элемента цепи, характеризующий его способность необратимо преобразовывать электрическую энергию в другие виды, называется активным сопротивлением, в отличие от цепей постоянного тока, где этот параметр называется просто сопротивлением.
Rакт.> Rпост.т.
При синусоидально изменяющемся токе в резистивных цепях напряжение пропорционально активному сопротивлению
i=ImSinωt, 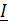 m=
m= 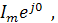 u=iR=RImSinωt
u=iR=RImSinωt
и достигает максимального значения одновременно с током, т.е. напряжение в резистивной цепи совпадают по фазе с током.
Произведение амплитуды тока и активного сопротивления дает амплитуду напряжения Um=RIm, тогда
u=UmSinωt, 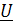 m=Um
m=Um 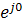 и Im=
и Im= 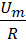 ,
,
аналогично для действующих значенийтока и напряжения
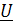 =U
=U 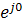 , I=
, I=  ,
, 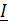 =
= 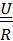 .
.
В индуктивных цепях напряжение пропорционально скорости изменения тока
u=Ls w:val="40"/><w:lang w:val="EN-US"/></w:rPr><m:t>di</m:t></m:r></m:num><m:den><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="40"/><w:sz-cs w:val="40"/><w:lang w:val="EN-US"/></w:rPr><m:t>dt</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 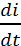 =L
=L 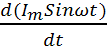 =ωLIm(Sinωt+
=ωLIm(Sinωt+ 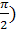 ,
,
следовательно, напряжение достигает максимального значения раньше тока на одну четверть периода. Т.к. в угловых единицах длительность периода составляет 2π радиан, то говорят, что напряжение в индуктивной цепи опережает ток на угол π/2. ωL имеет размерность сопротивления, называется индуктивным реактивным сопротивлением, обозначается символом ХL.
XL=ωL=2πfL , (2.1)
а произведение этого сопротивления и амплитуды тока дает амплитуду напряжения Um=ωLIm=XLIm=2πfLIm, тогда
u=UmSin(ωt + 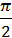 ),
), 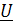 m=Um
m=Um 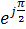 и Im=
и Im= 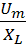 ,
,
аналогично для действующих значенийтока и напряжения
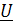 =U
=U 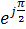 , I=
, I= 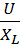 =
= 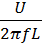 ,
, 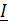 =
= 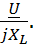
В цепях с емкостью ток пропорционален скорости изменения напряжения
i=C 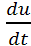 , u=
, u= 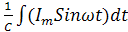 =
= 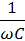 ImSin(ωt-
ImSin(ωt- 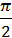 ),
),
следовательно, напряжение достигает максимального значения позже тока на одну четверть периода. В этом случае говорят, что напряжение в емкостной цепи отстает от тока на угол π/2. Дробь 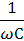 имеет размерность сопротивления, называется реактивным емкостным сопротивлением, обозначается символом ХС.
имеет размерность сопротивления, называется реактивным емкостным сопротивлением, обозначается символом ХС.
ХС=1/ωС=1/2πfC, (2.2)
а произведение этого сопротивления и амплитуды тока дает амплитуду напряжения Um=Im /ωC=Im / 2πfC, тогда
uC=UmSin(ωt – 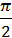 ),
), 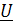 m=Um
m=Um 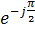 , и Im=
, и Im= 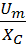 ,
,
аналогично для действующих значений напряжения и тока
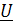 =U
=U 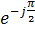 , I=
, I= 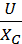 =
= 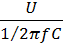 ,
, 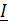 =
= 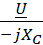 .
.
Таким образом, в цепях синусоидального тока активное сопротивление не зависит от частоты. Реактивное индуктивное сопротивление с увеличением частоты растет, а реактивное емкостное уменьшается.
Законы Кирхгофа для мгновенных значений токов и напряжений для цепей переменного тока справедливы в формулировках, данных для цепей постоянного тока на стр. 6. Для амплитудных и действующих значений напряжений и токов эти формулировки не применимы, т.к. максимальных значений на различных участках цепи эти величины достигают в разное время. В этих случаях суммировать нужно не численные значения токов и напряжений, а их векторы. Первый закон Кирхгофа для цепей синусоидального тока гласит:
«Геометрическая сумма токов, сходящихся в узле, равна нулю».
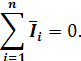
Второй закон Кирхгофа для цепей синусоидального тока гласит:
«Геометрическая сумма напряжений, действующих в контуре, равна нулю.
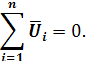
Дата добавления: 2016-02-04; просмотров: 2194;
