Методы расчета электрических цепей
Основные понятия и определения теории электрических цепей
Направленное движение электрических зарядов называется электрическим током. За положительное направление тока условно принято направление движения положительных зарядов. Электрический ток, не изменяющийся во времени, называется постоянным, его величина обозначается символом «I», а положительное направление указывается стрелкой, которая указывает направление уменьшения потенциала.
Совокупность устройств, предназначенная для получения электроэнергии, ее передачи и преобразования в другие виды, называется электрической цепью. Отдельное устройство, входящее в состав цепи и выполняющее в ней определенную функцию, называется элементом электрической цепи. Основными элементами цепей являются источники электрической энергии, соединительные провода, приемники, измерительные приборы, коммутационная и защитная аппаратура.
Токи в ветвях возникают под действием ЭДС источников, которые создаются в них в процессе преобразования иных видов энергии в электрическую, ее величина обозначается символом «Е», а положительное направление указывается стрелкой. За положительное направление ЭДС принято направление движения положительных зарядов внутри источника от отрицательного полюса к положительному. Стрелка ЭДС на электрических схемах указывает направление увеличения потенциала.
Элементы цепи делятся на активные и пассивные. Элемент, при работе которого в нем самом возникает ЭДС, называется активным.
Величины, характеризующие способность элементов преобразовывать электрическую энергию в другие виды, создавать свои собственные магнитные и электрические поля, называются параметрами.
Способность элемента цепи необратимо преобразовывать электрическую энергию в другие виды, зависит от параметра сопротивления R, чем больше этот параметр, тем большая энергия преобразуется элементом при заданной величине тока.
Величина, характеризующая способность элемента создавать во время работы свое собственное магнитное поле и накапливать в нем энергию, называется параметром индуктивности L, чем больше этот параметр, тем большая энергия накапливается в магнитном поле при заданной величине тока.
Способность элемента создавать во время работы свое собственное электрическое поле и накапливать в нем энергию, характеризуется параметром емкости С, чем больше этот параметр, тем большая энергия накапливается в электрическом поле при заданном напряжении.
Реальные приемники электроэнергии обладают всеми тремя параметрами, так же как реальные источники обладают двумя параметрами: ЭДС Е, которая характеризует способность источника поддерживать на концах цепи разность потенциалов и внутренним сопротивлением R0, которое характеризует способность источника необратимо преобразовывать часть вырабатываемой энергии в тепло.
Если элемент цепи обладает только одним параметром, он называется идеальным. При анализе электрического состояния электротехнических устройств реальные элементы, входящие в них, часто заменяют набором идеальных элементов, обладающих параметрами реальных.
Графическое изображение цепи с помощью идеальных элементов называется схемой замещения. Схема замещения является расчетной моделью электротехнического устройства. Элементы, которые не влияют на работу устройства в установившемся режиме (выключатели, предохранители, измерительные приборы), в схему замещения не включают, а параметры соединительных проводов считают нулевыми.
Элементы цепи могут быть соединены последовательно или параллельно. Если в каждом из них протекает один и тот же ток, то они соединены последовательно, если же они подключены к одной паре узлов, то параллельно.
Электрические цепи классифицируются по следующим признакам:
●по виду тока они делятся на цепи постоянного и переменного тока;
●по характеру параметров элементов цепи подразделяются на линейные и нелинейные. Цепь называется линейной, если параметры всех ее элементов не зависят от величин и направления тока и напряжения;
●по способу соединения элементов они делятся на простые и сложные. К простым относятся цепи, все элементы которых, соединены последовательно. К сложным относятся цепи с разветвлениями, которые могут быть с одним или несколькими источниками электроэнергии и в которых можно выделить ветви, узлы и контуры.
Ветвь - участок цепи, в любом сечении которого, протекает один и тот же ток.
Узел - точка соединения не менее трех ветвей.
Контур - любой замкнутый путь для электрического тока.
Электрическое состояние цепи или режим работы определяются значениями токов, протекающих в ее элементах, напряжения на зажимах и рассеиваемой в ней мощности. Если токи, напряжение и мощность, работающего электротехнического устройства, соответствуют значениям этих величин, указанных в паспорте заводом изготовителем, это означает, что устройство работает в номинальном режиме, который обеспечивает его наивысшие энергетические показатели и долговечность. Если же токи, напряжение и мощность не соответствуют паспортным, но отклонения находятся в допустимых пределах, то такой режим называется рабочим.
Ток в цепи, состоящей из источника с ЭДС Е c внутренним сопротивлением R0 и приемника с сопротивлением R, работающей в номинальном или рабочем режиме, описывается законом Ома:
I= 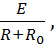 (1.1)
(1.1)
отсюда
I∙R=E-I∙R0.
Напряжение U на пассивном участке цепи, равное произведению I∙R, называется падением напряжения, его положительное направление совпадает с направлением тока и указывается на схеме стрелкой, которая указывает направление уменьшения потенциала.
U=I∙R,
тогда
U=E-I∙R0. (1.2)
Напряжение U на зажимах нагруженного источника меньше ЭДС на величину внутреннего падения напряжения I∙R0.
Из (1.1) следует, что при R=∞ I=0. Этот режим называется холостым ходом источника и, как видно из (1,2), в этом режиме напряжение на его зажимах равно ЭДС.
Если R=0, то величина тока будет ограничена только внутренним сопротивлением источника, он может достичь величин опасных для целостности источника, поэтому этот режим является аварийным и называется режимом короткого замыкания.
При равенстве сопротивлений приемника и источника, R= 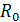 реализуется режим согласованной нагрузки, который используется только в технике слабых токов, т.к. в этом режиме 50% мощности источника рассеивается в нем самом.
реализуется режим согласованной нагрузки, который используется только в технике слабых токов, т.к. в этом режиме 50% мощности источника рассеивается в нем самом.
Методы расчета электрических цепей
Широкое распространение в практике инженерных расчетов получили следующие методы:
−непосредственного применения законов Кирхгофа;
−контурных токов;
−эквивалентного преобразования;
−наложения;
Метод непосредственного применения законов Кирхгофа является классическим приемом, используемым для анализа цепей любой сложности.
Первый закон Кирхгофа относится к узлу и гласит:
«Алгебраическая сумма токов, сходящихся в узле равна нулю»
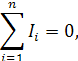
i-номер тока;
n-количество токов, сходящихся в узле.
Обычно, токи, подходящие к узлу, считают положительными.
Второй закон Кирхгофа относится к контуру и гласит:
«Алгебраическая сумма ЭДС, действующих в контуре, равна алгебраической сумме падений напряжений в том же контуре»:
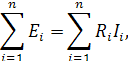
i- номер ветви контура;
n-число ветвей в контуре.
ЭДС и токи, направления которых совпадают с направлением обхода контуров, считаются положительными.
Для заданной электрической цепи составляется система линейных алгебраических уравнений первого порядка относительно неизвестных токов. По первому закону составляются уравнения для всех узлов, кроме одного. По второму закону для всех независимых контуров. Контур называется независимым, если он содержит хотя бы один элемент, не принадлежащий другим контурам. Общее число уравнений равно числу неизвестных токов.
Рассмотрим порядок расчета на примере цепи изображенной на рис.1.1.
Если по условию задачи внутренним сопротивлением источников R01 и R02 пренебречь нельзя, и они заданы, то их необходимо ввести в расчетную схему, включая последовательно с соответствующим источником.
| R1 |
| E2 |
| E1 |
| R2 |
| R01 |
| R02 |
| R1 |
| I3 |
| I1 |
| I2 |
| н.о. |
| b |
| a |
Рис.1.1 К расчету цепей методом непосредственного применения законов Кирхгофа
По признакам, данным в определении независимого контура можно выделить два независимых контура: R01E1R3R1 и R3R2E2R02, а по признакам, данным для узла, можно указать два узла: а и b.
●выбираем направление обхода и указываем его стрелкой снаружи схемы;
●направление токов в ветвях указываем стрелками на схеме произвольно;
●составляем уравнения Кирхгофа для узла a и для независимых контуров;
I1–I2+I3=0
(R01+R1)I1+0I2–R3I3=E1
0I1+(R2+R02)+R3I3= –E2
Полученная система уравнений может быть решена любым известным методом. Для удобства записи введем следующие обозначения:
a1, a2, a3 - коэффициенты при токе I1 в уравнениях 1, 2, 3;
b1, b2, b3 - коэффициенты при токе I2 в уравнениях 1, 2, 3;
c1, c2, c3,-коэффициенты при токе I3 в уравнениях 1, 2, 3;
d1, d2, d3-правая часть уравнений 1, 2, 3.
Теперь систему линейных уравнений можно переписать следующим образом:
a1I1+b1I2+c1I3=d1
a2I1+b2I2+c2I3=d2
a3I1+b3I2+c3I3=d3
При ручном расчете решение полученной системы уравнений может быть найдено по формулам Крамера:
Δ= 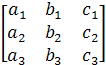 Δ1=
Δ1= 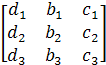 Δ2=
Δ2= 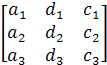 Δ3=
Δ3= 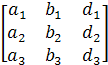
I1= 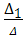 , I2=
, I2= 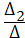 , I3=
, I3= 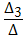
Δ= 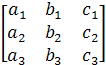 = a1b2c3+b1c2a3+c1a2b3 ─ a3b2c1 ─b3c2a1 ─ c3a2b1
= a1b2c3+b1c2a3+c1a2b3 ─ a3b2c1 ─b3c2a1 ─ c3a2b1
Δ1, Δ2, Δ3 рассчитываются аналогично.
При расчете на ЭВМ составляется матрица коэффициентов:
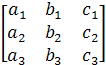 =
= 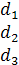
Если в исходных уравнениях некоторые токи отсутствуют, в матрицу коэффициентов проставляются соответствующие нули.
Проверка достоверности значений токов и их направлений осуществляется путем составления баланса мощностей.
Алгебраическая сумма мощностей источников равна сумме мощностей рассеиваемых в приемниках:
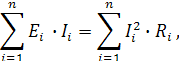
i−номер ветви цепи;
n−количество ветвей.
Произведение Ei∙Ii берется со знаком «+», если ток и ЭДС в данной ветви имеют одинаковое направление.
Метод контурных токовнаиболее распространенный способ анализа сложных электрических цепей. В его основе лежит второй закон Кирхгофа. Метод предполагает, что в каждом независимом контуре протекает собственный контурный ток, а ток каждой смежной (принадлежащей двум контурам сразу) ветви равен алгебраической сумме контурных токов, замыкающихся через эту ветвь. Ток в наружной ветви (принадлежащей только одному контуру) равен контурному току, замыкающемуся через эту ветвь.
Рассмотрим порядок расчета на примере цепи изображенной на рис.1.2.
●выбираем направление обхода и указываем его стрелкой снаружи схемы;
●направления контурных токов выбираем совпадающими с направлением обхода и указываем их стрелками на схеме ;
●составляем уравнения по второму закону Кирхгофа для всех независимых контуров, учитывая, что в резисторе R2 протекают контурные токи Iк2 и Iк3, навстречу друг другу; в резисторе R4 протекают контурные токи Iк1 и Iк3, навстречу друг другу; в резисторе R5 протекают контурные токи Iк1 и Iк2, также навстречу друг другу. В наружных ветвях R1, R6, R3 протекает по одному контурному току Iк1, Iк2, Iк3.
(R1+R5+R4) Iк1 ─ R5 Iк2 ─ R4 Iк3 = E1
─ R5 Iк1 + (R6+R2+R5) Iк2 ─ R2 Iк3= E2
─ R4 Iк1─R2 Iк2+(R2+ R3+ R4) Iк3= ─E3
| R3 |
| E2 |
| E1 |
| R6 |
| R1 |
| R2 |
| R4 |
| Ik3 |
| Ik1 |
| Ik2 |
| н.о. |
| R5 |
| E3 |
Рис.1.2. К расчету цепи методом контурных токов
Полученная система уравнений решается теми же способами, которые изложены в параграфе «Метод непосредственного применения законов Кирхгофа». Рассчитанные значения контурных токов позволяют найти токи в ветвях. В наружных ветвях, например в R1
I1= Iк1, если Iк1>0 и I1= ─ Iк1, если Iк1<0,
Аналогично находятся токи в других наружных ветвях I3 и I6.
В смежных ветвях R2, R4 и R5 протекает по два контурных тока. Например, в ветви R2 протекают контурные токи Iк2 и Iк3 навстречу друг другу, поэтому
I2= Iк2 ─ Iк3, если Iк2> Iк3 и I2= Iк3─ Iк2, если Iк3> Iк2,
за положительное направление тока I2 принимают направление большего контурного тока. Аналогично находятся токи I4 и I5.
Проверка правильности решения проводится так же, как при расчете методом непосредственного применения законов Кирхгофа. В некоторых случаях для одного из контуров рассчитывается потенциальная диаграмма, которая строится в прямоугольной системе координат. В ней по горизонтальной оси откладываются сопротивления между точкой, потенциал которой принят равным нулю и точками, в которых соединяются два любых элемента контура. При расчете потенциалов следует иметь в виду, что стрелка тока указывает направление уменьшения потенциала. Поэтому при переходе через резистор потенциал понижается на величину падения напряжения IiRi , если направление тока в резисторе совпадает с направлением обхода контура. Если это условие не выполняется, потенциал повышается на величину падения напряжения в резисторе.
Стрелка ЭДС указывает направление увеличения потенциала. Поэтому при переходе через источник энергии с ЭДС Еi потенциалскачком увеличивается на величину ЭДС источника Еi , если направление ЭДС совпадает с направлением обхода контура.Если это условие не выполняется, то потенциал скачком понижается на величину ЭДС. Т.к. работа по переносу заряда не зависит от формы пути, а зависит только от координат начальной и конечной точек, то для замкнутого контура диаграмма должна начинаться в точке с координатами φ=0, R=0 и заканчиваться в точке с координатами φ=0, R=Rк,
где Rк – полное сопротивление контура.
Метод эквивалентного преобразования используется для анализа цепей с одним источником энергии. Сущность его в том, что сложные участки цепи постепенно преобразуются в более простые по структуре. при этом токи и напряжения в непреобразованных частях цепи остаются неизменными. Рассмотрим порядок расчета на примере цепи изображенной на рис.1.3a, 3b.
| Е |
| R2 |
| R1 |
| R3 |
| а |
| b |
| (a) |
| I |
| Е |
| R23 |
| R1 |
| а |
| b |
| (b) |
| I |
Рис.1.3. К расчету цепей методом эквивалентного преобразования
Ветви R2 и R3 соединены параллельно, т. к. подключены к одной паре узлов а и b, и их эквивалентное сопротивление равно:
R23 = 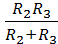 .
.
Теперь резисторы R2 и R3 на рис. 3a заменим одним эквивалентным R23 и цепь примет вид, представленный на рис. 3b.
Резисторы R1 и R23 включены последовательно и их эквивалентное сопротивление равно:
R123=R1+R23,
а ток I1, протекающий в цепи и напряжение на участке R23 можно найти, воспользовавшись законом Ома.
I1 = 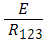 , U23=I1 R23 .
, U23=I1 R23 .
Токи в ветвях R2 и R3 также находятся по закону Ома:
I2= 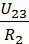 , I3=
, I3= 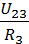 .
.
Метод наложения базируется на принципе суперпозиции. Применительно к электрическим цепям он гласит:
«Токи в ветвях цепи, содержащей несколько источников энергии, равны алгебраической сумме парциальных токов, образованных каждым источником в отдельности».
В соответствии с этим, из цепи последовательно исключают все источники кроме одного, и любым методом рассчитываются парциальные токи в ветвях. Для нахождения токов, возникающих в ветвях цепи при совместной работе всех источников, парциальные токи алгебраически складывают.
6.1.3. Задачи для самоподготовки по разделу «Цепи постоянного тока»
Задача 1.Найдите эквивалентное сопротивление трех последовательно включенных резисторов по 70 Ом.
Задача 2.Найдите эквивалентное сопротивление двух параллельно включенных резисторов по 70 Ом.
Задача 3.Найдите эквивалентное сопротивление трех параллельно включенных резисторов по 90 Ом.(Записав расчетную формулу, проверьте, не получается ли размерность Ом2 или Ом-1)
Задача 4.Найдите эквивалентное сопротивление четырех параллельно включенных резисторов по 120 Ом.
Задача 5.Найдите эквивалентное сопротивление трех параллельно включенных резисторов с R1=3 Ом, R2=6 Ом, R3=2 Ом.
Задача 6.Найдите эквивалентное сопротивление цепи, составленной из двух параллельно включенных резисторов по 20 Ом, последовательно соединенных с резистором сопротивлением 10 Ом.
Задача 7.Найдите эквивалентное сопротивление цепи, составленной из трех параллельно включенных резисторов по 30 Ом, последовательно соединенными с двумя параллельно включенными резисторами по 20 Ом.
Задача 8.Резистор с R=20 Ом поставлен под напряжение 45 В. Найдите ток, протекающий в резисторе.
Задача 9.Два последовательно включенных резистора с R1=20 Ом и R2=30 Ом поставлены под напряжение 100 В. Найдите ток, протекающий в резисторах.
Задача 10.Два параллельно включенных резистора с R1=20 Ом и R2=30 Ом поставлены под напряжение 120 В. Найдите токи, протекающие в каждом резисторе.
Задача 11.Два параллельно включенных резистора с R1=20 Ом и R2=30 Ом поставлены под напряжение 120 В. Найдите ток источника энергии.
Задача 12.По двум последовательно соединенным резисторам с сопротивлениями R1=20 Ом, R2=30 Ом протекает ток в 3А. Найдите напряжения на резисторах.
Задача 13.Найдите напряжения на каждом из двух последовательно соединенных резисторах с R1=3 Ом, R2=6 Ом, подключенных к источнику с Е=25 В и внутренним сопротивлением R0=1 Ом.
Задача 14.В неразветвленной части цепи, составленной из источника Е и трех параллельно включенных резисторов по 6 Ом, течет ток в 10 А. Найдите напряжение источника.
Задача 15.Цепь, образованная двумя параллельно включенными резисторами с R1=20 Ом и R2=30 Ом, соединенными последовательно с резистором R3=6 Ом, поставлена под напряжение 36 В. Начертите цепь и найдите напряжения на каждом резисторе.
Задача 16.Цепь, образованная двумя параллельно включенными резисторами R1=6 Ом и R2=3 Ом, соединенными последовательно с резистором R3=10 Ом, поставлена под напряжение U=12 В. Начертите цепь и найдите ток в резисторе R3.
Задача 17. Цепь, образованная тремя параллельно включенными резисторами R1=30 Ом, R2=20 Ом, R3=12 Ом, соединенными последовательно с резистором R4=4 Ом, поставлена под напряжение U=40 В. Начертите цепь и найдите ток в резисторе R3.
Задача 18.Резистор, имеющий сопротивление 6 Ом, подключен к источнику с напряжением 12 В. Найдите мощность потребляемую резистором.
Задача 19.Цепь, образованная двумя последовательно включенными резисторами R1=6 Ом и R2=12 Ом, поставлена под напряжение U=36 В. Найдите мощности, рассеивающиеся в резисторах и мощность отдаваемую источником.
Задача 20. Цепь, образованная двумя последовательно включенными резисторами R1=2 Ом и R2=3,5 Ом подключена к источнику с ЭДС Е=12 В и внутренним сопротивлением R0=0,5 Ом. Начертите цепь и найдите мощности, рассеиваемые в резисторах R1 и R2, составьте баланс мощностей.
Задача 21.Цепь, образованная двумя параллельно включенными резисторами
R1=20 Ом и R2=30 Ом, соединенными последовательно с резистором R3=6 Ом, поставлена под напряжение 36 В. Найдите мощности, рассеиваемые в резисторах.
6.1.4. Тест для самопроверки по разделу «Цепи постоянного тока»
1. Узлом электрической цепи называется….
2. Первый закон Кирхгофа гласит…..
3. Номинальный режим работы электротехнического устройства это….
4. Цепь называется нелинейной, если…..
5. Эквивалентное сопротивление двух параллельно включенных резисторов с сопротивлениями 6 Ом и 3 Ом равно…..
6. Эквивалентное сопротивление трех параллельно включенных резисторов вычисляют по формуле….
7. В параллельных ветвях протекают токи: 10А и 15А, а в неразветвленной части….
8. Параметр емкости характеризует способность элемента цепи….
9. На схемах замещения реальный источник энергии изображают символами….
10. При расчете цепи применением законов Кирхгофа по первому закону составляют столько уравнений….
11. ЭДС источника это…..
12. Из перечня: источник, предохранитель, приемник в схему замещения не включают….
13. Эквивалентное сопротивление трех последовательно включенных резисторов по 18 Ом равно…
14. В резисторе с сопротивлением 10 Ом рассеивается мощность 90 Вт и течет ток….
15. Элемент цепи называется идеальным, если….
16. В уравнении баланса мощностей произведение Ei Ii входит со знаком «+» если….
17. Отношение токов I1/I2 двух параллельно включенных резисторов с сопротивлениями R1 =2 Ом , R2 =10 Ом равно….
18. Параметр сопротивления R характеризует свойство элемента цепи….
19. Количество уравнений необходимых для расчета цепи применением законов Кирхгофа определяется по формуле….
20. На источнике с Е=10 В при токе I=1 A напряжение U=9В, а его внутреннее сопротивление….
21. За положительное направление напряжения принято…..
22. В резисторе с сопротивлением R=10 Ом рассеивается мощность 490 Вт и протекает ток….
23. Токи в смежных ветвях, при расчете методом контурных токов, находят как….
24. Мощность, развиваемая источником, максимальна в режиме…
25. Параметр ЭДС характеризует свойство источника….
Дата добавления: 2016-02-04; просмотров: 1967;
