Расчет сложных цепей синусоидального тока символическим методом
Символический метод расчета электрических цепей основан на описании векторов комплексными числами, что позволяет заменить геометрическое сложение векторов суммированием комплексных чисел, соответствующих векторам. Цепи с одним источником энергии целесообразно рассчитывать методом эквивалентного преобразования. При расчете следует придерживаться следующей последовательности.
1. На схеме указать положительное направление напряжения на зажимах источника и положительное направление токов во всех ветвях.
2. Определить индуктивные и емкостные сопротивления ветвей, имеющих соответственные реактивные приемники.
3. Записать комплексы полных сопротивлений каждой ветви.
4. Рассчитать комплекс полного сопротивления параллельного участка.
5. Рассчитать комплекс полного сопротивления цепи.
6. Рассчитать комплекс тока в неразветвленной части цепи.
7. Рассчитать комплекс напряжения на неразветвленном участке цепи.
8. Рассчитать комплекс напряжения на параллельном участке цепи.
9. Рассчитать комплексы токов параллельных ветвей.
10. Составить баланс комплексных мощностей.
11. Построить векторные диаграммы напряжений и токов.
Рассмотрим расчет на примере цепи изображенной на рис. 2.8.
| u |
| R1 |
| С1 |
| С2 |
| С3 |
| R2 |
| R3 |
| L1 |
| L2 |
| L3 |
| i1 |
| i2 |
| i3 |
Рис. 2.8. Расчетная цепь
1. Положительное направление напряжения на зажимах источника указывается произвольно. Положительное направление токов в ветвях указывается в соответствии с выбранным направлением напряжения.
2. Индуктивные 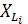 и емкостные
и емкостные 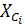 сопротивления реактивных элементов находятся по формулам (2.1) и (2.2). При расчете реактивных сопротивлений индуктивности подставляются в формулы в генри (Гн), а емкости в фарадах (Ф).
сопротивления реактивных элементов находятся по формулам (2.1) и (2.2). При расчете реактивных сопротивлений индуктивности подставляются в формулы в генри (Гн), а емкости в фарадах (Ф).
3. Комплексы полных сопротивлений ветвей Zi записываются в соответствии с (2.7). При отсутствии в i ветви одного или двух приемников в формулу (2.7) вместо их сопротивлений проставляются нули.
4. Комплекс полного сопротивления двух параллельных ветвей рассчитывается по формуле аналогичной для расчета эквивалентного сопротивления двух параллельных ветвей цепи постоянного тока. Но вместо R, в нее входят соответствующие комплексы полных сопротивлений Zi.
Z23= 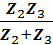 .
.
При подстановке значений комплексов полных сопротивлений ветвей в формулу расчета Z23 для числителя следует использовать показательную форму записи, а для знаменателя алгебраическую. После вычисления знаменателя его необходимо перевести в показательную форму записи, а после вычисления дроби результат следует перевести в алгебраическую форму, используя тригонометрическую форму записи комплексного числа.
5. Комплекс полного сопротивления всей цепи находится суммированием комплексов Z1 и Z23.
Zэкв..=Z1+Z23.
6. Комплекс тока в неразветвленной части цепи находится на основании закона Ома , записанного в комплексной форме (2.9). Т.к. начальная фаза приложенного напряжения обычно не задается, то для упрощения расчетов ее можно принять равной нулю.
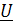 =
= 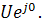
7. Комплексы напряжений на неразветвленном и параллельных участках цепи легко вычислить, пользуясь законом Ома для участка цепи, т.к. 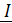 1, Z1 и Z23 известны:
1, Z1 и Z23 известны:
t wx:val="Cambria Math"/><w:i/><w:sz-cs w:val="28"/><w:vertAlign w:val="subscript"/><w:lang w:val="EN-US"/></w:rPr><m:t>U</m:t></m:r></m:e></m:bar></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 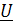 1=
1= 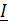 1
1 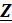 1, t wx:val="Cambria Math"/><w:i/><w:sz-cs w:val="28"/><w:vertAlign w:val="subscript"/><w:lang w:val="EN-US"/></w:rPr><m:t>U</m:t></m:r></m:e></m:bar></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
1, t wx:val="Cambria Math"/><w:i/><w:sz-cs w:val="28"/><w:vertAlign w:val="subscript"/><w:lang w:val="EN-US"/></w:rPr><m:t>U</m:t></m:r></m:e></m:bar></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 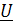 23=
23= 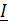 1
1 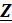 23.
23.
8. Комплексы токов в параллельных ветвях можно рассчитать, пользуясь законом Ома, т.к. комплексы полных сопротивлений параллельных ветвей известны, а комплекс напряжения на параллельном участке цепи определен в предыдущем пункте:
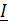 2=
2= 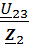 ,
, 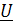 3=
3= 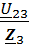
9. В соответствии с законом сохранения энергии, комплекс мощности источника должен быть равен сумме комплексов мощностей всех ветвей цепи:
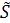 =
= 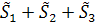 ,
, 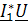 =
= 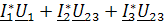 ,
,
где 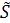 -комплексная мощность источника;
-комплексная мощность источника;
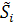 -комплексная мощность i ветви;
-комплексная мощность i ветви;
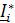 -сопряженный комплекс тока (комплекс тока, у которого знак перед jφ изменен на противоположный).
-сопряженный комплекс тока (комплекс тока, у которого знак перед jφ изменен на противоположный).
При расчете мощностей результат необходимо записать в алгебраической форме. Действительная часть есть активная мощность, а мнимая реактивная. Расхождение в балансах активных и реактивных мощностей при правильном решении задачи не должно превышать 2%.
10. Векторную диаграмму можно начать строить с вектора напряжения 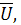 приложенного к зажимам цепи. Т.к. его начальная фаза была принята равной нулю, он откладывается вдоль положительного направления оси действительных величин. Векторы напряжений
приложенного к зажимам цепи. Т.к. его начальная фаза была принята равной нулю, он откладывается вдоль положительного направления оси действительных величин. Векторы напряжений 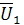 и
и 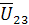 строятся под соответствующими углами φi по отношению к оси действительных величин. Отрицательные углы откладываются по направлению вращения часовой стрелки, а положительные - против часовой. Аналогично строятся векторы токов в ветвях. При правильно определенных комплексах токов и напряжений вектор тока в неразветвленной части цепи
строятся под соответствующими углами φi по отношению к оси действительных величин. Отрицательные углы откладываются по направлению вращения часовой стрелки, а положительные - против часовой. Аналогично строятся векторы токов в ветвях. При правильно определенных комплексах токов и напряжений вектор тока в неразветвленной части цепи 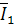 должен быть диагональю параллелограмма, двумя сторонами которого являются векторы токов в параллельных ветвях
должен быть диагональю параллелограмма, двумя сторонами которого являются векторы токов в параллельных ветвях 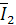 и
и 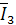 . Вектор приложенного напряжения
. Вектор приложенного напряжения 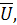 должен быть диагональю параллелограмма, сторонами которого являются векторы
должен быть диагональю параллелограмма, сторонами которого являются векторы 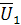 и
и 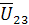 .
.
6.2.6. Задачи для самоподготовки по разделу «Однофазные цепи»
Дата добавления: 2016-02-04; просмотров: 2512;
