Определение оптимальных режимов работы датчика

На величину выходных параметров устройства для измерения изменений толщины изделий могут оказывать существенное влияние различные факторы: соотношение геометрических размеров датчиков, изделия, частота намагничивающего тока, степень идентичности датчиков, материал магнитопроводов, изменение удельной электрической проводимости, величина воздушного зазора между преобразователем и изделием.

Естественно, для того чтобы измерять толщину изделия, необходимо полностью его промагнитить. С этой точки зрения, глубина проникновения магнитного поля δ должна быть больше толщины изделия. Однако случай δ >> а приводит к значительному снижению чувствительности преобразователя. Оценки показывают, что достаточно высокая чувствительность устройства достижима при условии 0,3 ≤ а/δ ≤ 0,77. При этом необходимо обеспечить выполнение ограничений на соотношение геометрических размеров магнитопровода и изделия, связанных с распространением магнитного поля в изделии и за ним (с ≥ d, d = a + a₁). Увеличение толщины магнитопровода приводит к росту чувствительности устройства, однако, существует ограничение и на этот размер, связанное с требуемой площадью контролируемого участка изделия, соприкасаемой с рабочей поверхностью магнитопровода.

Даже из физических соображений ясно, что рассматриваемый электромагнитный преобразователь должен иметь оптимальный режим работы по такому параметру, как частота намагничивающего тока (или возбуждающего магнитного поля). Действительно, при низких частотах (δ >> а) чувствительность устройства мала. Та же ситуация должна наблюдаться и при высоких частотах, когда δ << а. Отсюда следует, что должен существовать такой частотный диапазон, при котором чувствительность датчика к изменению толщины будет максимальной.

Достаточно простое приближенное расчетное соотношение для оптимальной частоты преобразователя по величине наибольшей относительной чувствительности к изменению толщины изделия можно получить из выражения (1.10) при условии а/δ < 1. В этом случае

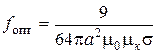. (1.14)

Из формулы (1.14) следует, что в зависимости от материалов используемого магнитопровода и изделия существуют определенные ограничения на минимальную толщину эталонного образца а. Если применять в качестве материала магнитопровода феррит, то даже при малой исходной толщине изделия измерения на оптимальных частотах не представляют особых трудностей. К примеру, при а = 0,2 мм для медного листа f_опт ≈ 16 кГц. В случае использования шихтованного магнитопровода, набранного из ферромагнитных пластин (конструкции которого будут рассмотрены ниже), имеется максимальное значение частоты, при которой еще не сильно выражен поверхностный эффект в отдельных пластинах магнитопровода. Таким образом, есть верхний предел по частоте для шихтованного магнитопровода, который зависит от толщины и материала используемых пластин. Например, для пластин, выполненных из электротехнической стали толщиной 0,35 мм каждая, наибольшая частота составляет 4–5 кГц. Если принять эту частоту в качестве оптимальной, то из выражения (2.14) следует ограничение на минимальный размер исходной толщины изделия. К примеру, для медного изделия (σ = 5,6×10^–7См/м) и частоте 5 кГц a_min = 0,35 мм, а для изделия из алюминиевого сплава
(σ = 1,72∙10^–7См/м) a_min = 0,6мм. Следует отметить, что ограничение на наибольшее значение исходной толщины изделия а связано с требуемым отношением полезного сигнала к сигналу небаланса Е_ндвух датчиков, помещённых на идентичные изделия. В практически важном случае Dа/а₁ << 1 наибольшую исходную толщину изделия можно определить из выражения

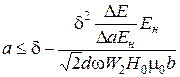. (1.15)

Порядок вычисления этой величины следующий. Измерив значение сигнала небаланса Е_ни считая, что полезный сигнал ∆Е должен превышать величину Е_н хотя бы на порядок, можно определять а, которое соответствует минимальным заданным приращениям толщины ∆а.

При использовании формулы (1.10) необходимо также ввести ограничение на наибольшее изменение толщины∆а. В этом случае предельно допустимая величина ∆а связана с погрешностью разложений. Простую оценку такой погрешности можно получить из соотношения

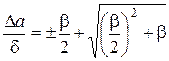, (1.16)

где β – задаваемая погрешность разложения; верхний и нижний знаки соответствуют уменьшению и увеличению толщины изделия. Например, при β= 3 %величины допустимых относительных приращений ∆а/δ толщин изделий составляют 0,19 и 0,16 при уменьшении и увеличении толщины а.

Увеличение величины напряженности магнитного поля Н₀в зазоре магнитопровода играет важную роль в повышении чувствительности устройства. Однако такое увеличение должно быть конечным и связано, по-видимому, с эффектами нагрева изделия вихревыми токами, которые могут привести к изменению характеристик изделия. Степень нагрева изделия зависит от величины Н₀, закона распределения плотности вихревых токов, материала изделия, состояния его поверхности и др. Приведенное выше выражение (1.13), описывающее распределение плотности вихревых токов, недостаточно для оценки предельной величины Н₀. Более целесообразно оценивать эту величину по значению плотности тока усредненной по толщине изделия, так как в случае толщинометрии δ > а. Используя соотношение (1.13), можно получить выражение для такой усредненной плотности тока, модуль которой имеет вид

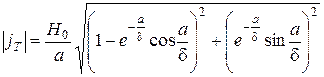. (1.17)

Исходя из формулы (1.17), можно для каждого материала определить предельную величину Н₀по допустимой плотности вихревых токов.

Определение допустимых величин плотностей токов для различных материалов с точки зрения минимального нагрева связано с решением сложных уравнений диффузии тепла и теплового баланса проводящего изделия. Для решения вопроса выбора диапазона допустимого изменения Н₀, исходя из компромиссных решений достижения сравнительно высокой чувствительности и слабого влияния тепловых эффектов вихревых токов, можно использовать справочные данные по допустимым плотностям тока для различных материалов. Например, если принять для медной пластины допустимую плотность тока j_доп = 2 А/мм² , то для предельного случая а/δ = 0,77; а = 0,35 мм и f = 5000 Гц (шихтованный магнитопровод) наибольшее значение напряжённости магнитного поля в зазоре магнитопровода Н_доп составляет 944 А/м. При увеличении толщины изделия и при том же отношении а/δ, как видно из выражения (1.17), для достижения таких же допустимых плотностей вихревых токов следует использовать более высокие значения напряженности магнитного поля, что, в свою очередь, приведет к увеличению чувствительности устройства.

Мешающими параметрами при измерении приращения толщин являются удельная электрическая проводимость (электропроводность) σизделия и воздушный зазор между первичным преобразователем и поверхностью изделия.

На рис.1.3 приведены расчетные кривые зависимостей относительных значений выходных ЭДС дифференциального индуктивного преобразователя от величины δ при изменении удельной электрической проводимости (ω = const). Кривые построены для значений а = 10^–2 м, а₁ = 4∙10^–3 м, ∆а = 10^–3 м в случае уменьшения толщины (кривая 1), а = 6∙10^–3 м, а₁ = 8∙10^–3 м, ∆а = 10^–3 м – для увеличения толщины (кривая 2).

Из графических зависимостей (рис.1.3) видно, что наибольшее влияние σ на результаты измерений наступает при глубинах проникновения переменного магнитного поля δ ≈ а (кривая 1).

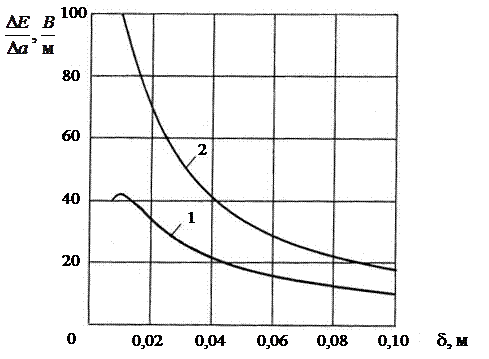
Рисунок 1.3 – Зависимость относительной ЭДС от δ при изменении
удельной электрической проводимости изделия

Однако в окрестности этого значения δ воздействие изменения удельной электрической проводимости минимально. В благоприятном, с точки зрения оптимальных режимов работы устройства, диапазоне изменений а/δвлияние изменения величины σ также мало. К примеру, при а/δ= 0,6 (а = 10^–2 м), изменение сигнала ∆Е/∆а не превышает 2,0 %, а для а/δ= 0,35 (а = 6∙10^–3 м), ∆Е/∆а изменяется на 2,9 %при изменении σна 10 % в обоих случаях. Следует отметить, что увеличение δприводит к уменьшению влияния удельной электрической проводимости на результаты измерений приращений толщин.

Как было указано выше, преобразователь помещается непосредственно на испытуемое изделие. Во многих случаях необходимо предусмотреть наличие небольшого зазора l_з между полюсами магнитопровода и изделием. В силу того что в рассматриваемых преобразователях воздушный зазор магнитопровода, определяемый средней силовой линией, значительно превышает величину l_з, не следует ожидать большого воздействия последней на результаты измерений. При учетеl_з значение разностной ЭДС уменьшится на величину 2∆Еl_з /(с + d). Например, для датчиков с величиной с + d = 28∙10^–3 м наличие зазора l_з = 0,5∙10^–3 м приводит к уменьшению выходной ЭДС на 3,6 %.