Оценка погрешностей измерений толщин изделий

При анализе погрешностей измерений необходимо учитывать то, что метод измерения, положенный в основу работы дифференциального толщиномера, является косвенным. Отсюда следует, что погрешности измерений величины приращений толщины изделий нужно определять, пользуясь результатами обработки косвенных измерений. При условии ∆а/δ<<1(практически важный случай) окончательные формулы для оценки погрешностей не будут отличаться в случаях увеличения и уменьшения толщины изделия. Тогда, воспользовавшись выражениями (1.10)– (1.12), получим формулу для результирующей относительной погрешности измерения приращений толщины:

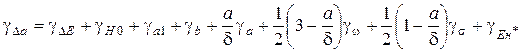, (1.18)

где γ_∆Е, γ_Н0, γ_а1, γ_b, γ_а, γ_ω, γ_σ –относительные погрешности соответствующих параметров; γ_Ен* – относительная погрешность, вызванная сигналом небаланса, получаемого на двух идентичных эталонных изделиях; γ_Ен* = Е_н /∆Е_min; ∆Е_min – минимальный полезный сигнал; величины а и δ соответствуют заданным толщинам эталонного изделия и глубинам проникновения магнитного поля в эталонное изделие.

Относительную погрешность определения средней напряженности магнитного поля определим, исходя из выражения (1.6):

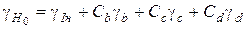, (1.19)

гдеγ_Iн, γ_b, γ_c, γ_d – относительные погрешности измерения параметров I_н, b, с, d;

;

;

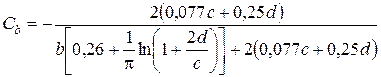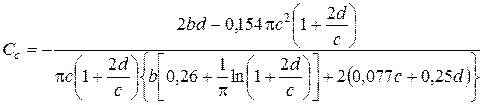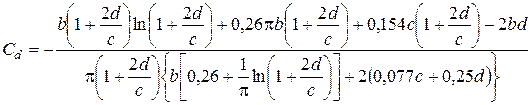
– коэффициенты влияния.

Поскольку величину Н₀ можно для каждого датчика определить экспериментально при помощи контура заданных размеров, подключенного к вольтметру, то в этом случае погрешность γ_Н0 будет определяться классом точности используемого вольтметра.

Поскольку составляющие результирующей погрешности не зависят друг от друга и носят случайный характер, то, как показано в работе [13], в этом случае целесообразно оценивать величину погрешности косвенных измерений при доверительной вероятности 0,95, исходя из выражения

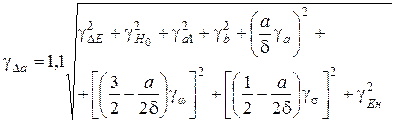. (1.20)

Из (1.20) следует, что погрешности измерения толщины изделия некритичны к разбросам такого важного мешающего фактора, как удельная электрическая проводимость материала изделия. При сравнительно больших приращениях толщины к погрешности γ_∆аследует прибавить еще методическую погрешность, связанную с применяемым разложением (1.16). Так, например, в случае уменьшения толщины изделия на величину ∆а = 3∙10^–3 м (а = 10^–2 м, δ = 17,2∙10^–3 м) методическая погрешность не превышает 3 %, а для случая увеличения толщины на такую же величину (а = 6∙10^–3 м, δ = 17,2∙10^–3 м) эта погрешность не более 4 %.

Величина погрешности, рассчитанная по формуле (1.20), является максимальной. Численное значение этой погрешности можно уменьшить за счет уточнения результатов путем обработки данных многократных измерений.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1 Какие условия позволяют получить простые соотношения для выходного сигнала измерителя толщины изделия?

2. Какие факторы влияют на величину выходного сигнала измерителя толщины?

3. Что определяет рабочую частоту толщиномера?

4. С чем связано ограничение на максимальную величину напряженности магнитного поля?

5. Как рассчитать наибольшую исходную толщину изделия?

6. Как рассчитать предельно допустимое изменение толщины изделия?