Теория работы преобразователя
ДИФФЕРЕНЦИАЛЬНЫЙ ЭЛЕКТРОМАГНИТНЫЙ ПРЕОБРАЗОВАТЕЛЬ ДЛЯ ИЗМЕРЕНИЯ ПРИРАЩЕНИЙ ТОЛЩИНЫ ТРУБЧАТЫХ И ЛИСТОВЫХ НЕМАГНИТНЫХ ИЗДЕЛИЙ
Теория работы преобразователя
Рассмотрим индуктивный преобразователь с разомкнутым магнитопроводом для измерения толщин немагнитных листовых и трубчатых изделий. Чувствительность одного датчика к измеряемому параметру оказывается низкой. Для ее увеличения два одинаковых датчика включены по дифференциальной схеме (рис.1.1). Рабочий РД и компенсационный КД датчики имеют по две идентичные намагничивающие и измерительные обмотки, размещенные на магнитопроводах с зазорами. Рабочий датчик устанавливается на испытуемое изделие ИИ, а компенсационный – на образцовое ОИ. Намагничивающие обмотки с числами витков W1 включаются последовательно-согласно и питаются от генератора G. Величина тока в намагничивающей цепи регулируется сопротивлением RC и измеряется амперметром РА. Измерительные обмотки с количеством витков W2 включаются последовательно-встречно, разностный сигнал ЭДС ∆Е измеряется вольтметром PV. Знак приращения толщины изделия определяется при помощи фазочувствительного вольтметра.
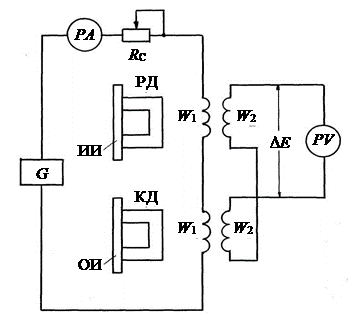
Рисунок 1.1 – Электрическая схема включения преобразователей
На рис.1.2 а, б показано размещение магнитопроводов рабочего и компенсационного датчиков на листовом и трубчатом изделиях. Даны обозначения: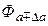 
, 
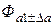и Фр1 – мгновенные значения потоков в исследуемом изделии, в слое воздуха за изделием и рассеяния; Фа, Фа1, и Фр2, – мгновенные значения потоков в образцовом изделии, в слое воздуха за ним и рассеяния; а и а1 – толщины изделия и слоя воздуха за ним, ограничивающие соответствующие потоки; ∆a – изменение толщины изделия; знаки 
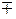соответствуют уменьшению и увеличению толщины изделия; b – толщина магнитопровода; c – расстояние между полюсами магнитопровода; d – ширина полюса магнитопровода.
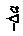
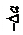
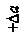
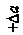
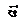
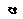
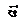
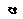
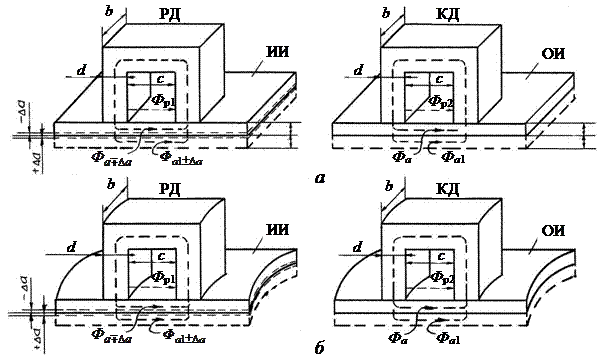
Рисунок 1.2 – Размещение магнитопроводов рабочего и компенсационного
датчиков на листовом (а) и трубчатом (б) изделиях
Назовем 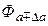+ 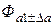эффективным потоком рабочего датчика, а Фа + Фа1 – эффективным потоком образцового датчика. Примем некоторые допущения. Поскольку воздушный зазор в магнитопроводе сравнительно велик, эффективный магнитный поток будет определяться магнитным сопротивлением зазора, а не сопротивлением магнитопровода. Кроме эффективного потока, существуют потоки рассеяния, расчет которых можно провести, используя работу [9]. Будем считать, что практически весь эффективный поток ограничивается размером ширины полюса магнитопровода d = a + a1. Последнее подтверждается теоретическими и экспериментальными данными [7,9,10].
Выражение для мгновенного значения разностной ЭДС во вторичных обмотках датчиков имеет вид [121]
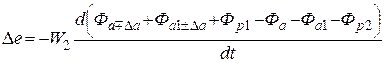. (1.1)
Так как рабочий и компенсационный датчики выполнены идентичными и включаются по дифференциальной схеме, можно считать, что потоки рассеяния будут одинаковыми (то естьФр1 = Фр2) и в выражении (1.1) взаимно компенсируются. Это относится к немагнитному изделию, поскольку магнитные потоки, связанные с вихревыми токами, значительно меньше потоков рассеяния.
В основу расчета эффективных потоков датчиков положены законы распространения электромагнитного поля в случае падающей плоской электромагнитной волны [11]. Воспользовавшись выражением для напряженности магнитного поля в теле эталонного и исследуемого изделий и за ними, с учетом изменения толщины последнего, определим соответствующие магнитные потоки. При этом выражения для них имеетвид:
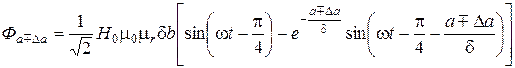, (1.2)
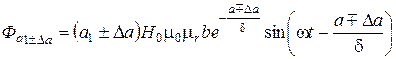, (1.3)
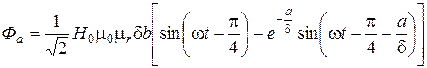, (1.4)
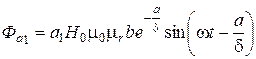, (1.5)
где H0 – средняя напряженность магнитного поля в воздушном зазоре датчика;
μ0 – магнитная постоянная (4π∙10–7 Гн/м) ;
μr – относительная магнитная проницаемость изделия;
ω – циклическая частота;
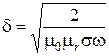– глубина проникновения магнитного поля в среду;
σ– удельная электрическая проводимость материала изделия.
Данные соотношения получены при условии равенства относительных магнитных проницаемостей (μr = 1) и удельных электропроводностей материалов исследуемого и образцового изделий. Это можно выполнить на практике с помощью подбора образцовых изделий по значению σ, соответствующей удельной электрической проводимости исследуемого изделия. Если размеры изделия достаточно велики, то оба датчика можно разместить на нем, но при этом должна быть известна толщина изделия в месте размещения образцового датчика.
Воспользовавшись результатами работ [9,10], можно получить выражение для значения средней напряженности магнитного поля в воздушном зазоре датчика [12,14]
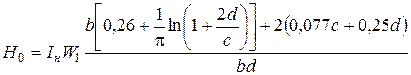, (1.6)
где IH– величина тока в намагничивающей цепи.
Подставив значений магнитных потоков (1.2–1.5) в выражение (1.1), получим формулу для мгновенного значения разностной ЭДС
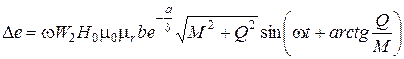, (1.7)
где
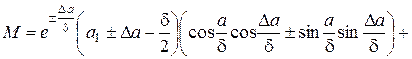
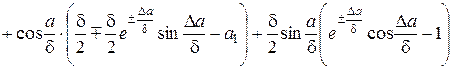; (1.8)
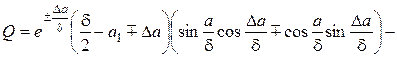
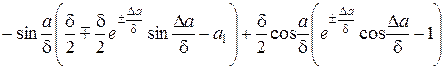. (1.9)
Выражения (1.7–1.9) значительно упрощается при условии ∆а/δ << 1,что соответствует небольшим изменениям толщины исследуемого изделия относительно образцового или малым частотам питающего тока. В этом случае формула для эффективного значения разностной ЭДС имеет вид [12]
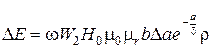, (1.10)
Величина ρ рассчитывается из следующих соотношений, при уменьшении толщины исследуемого изделия относительно образцового:
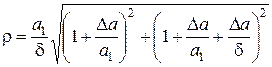, (1.11)
при ее увеличении
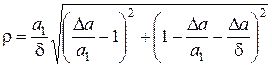. (1.12)
Использование выражений (1.7–1.12) для измерения толщин трубчатых изделий справедливо при условии b/(pD) < 1(D – наружный диаметр трубчатого изделия).
Следует отметить, что для толщинометрии различных изделий можно было бы использовать и фазовые измерения (см. выражения 1.7–1.9). Однако численные оценки, проведенные по точным и приближенным выражениям для фазовых углов, показывают, что для различных исходных толщин разрешающая способность фазовых измерений значительно ниже амплитудных при тех же изменениях ∆a. К этому можно также добавить неудобство проведения фазовых измерений, связанное со сравнительно низкой точностью измерителей фазовых сдвигов, требованиями к минимальным входным сигналам и другие.
Поскольку, наряду с магнитным потоком в изделии важным зондирующим параметром является величина вихревого тока, создаваемого этим потоком, то имеет смысл привести выражение для распределения плотности вихревых токовjт внутри изделия. Воспользовавшись результатами работы [11], можно получить соотношение для jт с учетом полученной выше Н0:
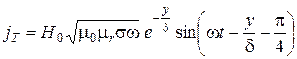(2.13)
где у– текущая координата толщины изделия (у = 0 на поверхности образца в месте расположения датчика).
Дата добавления: 2016-01-30; просмотров: 560;