Средняя длина свободного пробега
Будем считать молекулы шарами с диаметром d, равным эффективному диаметру (25.1). Будем также считать, что все молекулы движутся в случайных направлениях с одинаковой скоростью, равной средней скорости <v>. Тогда средняя длина свободного пробега λ будет связана со средней скоростью молекул <v> простой формулой:
здесь τ - среднее время свободного пробега, т.е. среднее время, в течение которого молекула движется между двумя последовательными соударениями. Иными словами - за время молекула в среднем испытывает одно столкновение.
Величина τ зависит от числа молекул в единице объема n (концентрации), их эффективного диаметра d и от средней относительной скорости vотнсталкивающихся молекул.
Средняя относительная скорость движения молекул vотн больше, чем их средняя скорость <v>. Можно показать, что:

Рис. 6.2
На рисунке 6.2 проиллюстрирован процесс столкновения двух молекул в системе отсчета, где молекула 2 покоится. Молекула 1 может столкнуться с молекулой 2, если центр молекулы 2 расположен от линии движения молекулы 1 не дальше чем d - эффективный диаметр молекул. Это значит, что в объеме изображенного на рисунке цилиндра в среднем должна находиться одна молекула. Обозначим площадь основания этого цилиндра буквойσ. Величина σ называется полным сечением столкновения двух молекул. Объем будет равен σ · (vотн · τ). Умножив этот объем на концентрацию n, мы получим число молекул N в объеме изображенного цилиндра, которое, как сказано выше, должно быть равно единице (одно столкновение за время τ!), т.е.
Откуда
Подставляя сюда , получим:
Подставив в формулу для λ из (6.1) величину τ из (6.3), получим формулу, связывающую длину свободного пробега с концентрацией молекул и полным сечением столкновения σ:
Напомним, что σ = π · d2, а d - эффективный диаметр молекулы, он уменьшается с ростом температуры.
Так как по формуле (1.5):
p = nkT,
то для λ получим:
Оценим λ для газа, находящегося при нормальных условиях: (p = 1 атм ≈ 105 Па, T = 0oС = 273 К).
Примем, что эффективный диаметр молекул d ≈ 2 · 10-10 м, тогда
Таким образом λ >> d, т.е. при обычных условиях молекула пролетает относительно большое расстояние прежде, чем столкнется с другой молекулой.
25) явления переноса
1. ления переноса объединяют группу процессов, связанных с неоднородностями плотности, температуры или скорости упорядоченного перемещения отдельных слоев вещества. Выравнивание неоднородностей приводит к возникновению явления переноса.
Явления переноса в газах и жидкостях состоят в том, что в этих веществах возникает упорядоченный, направленный перенос массы (диффузия), импульса (внутренняя энергия) и внутренней энергии (теплопроводность). При этом в газах нарушается полная хаотичность движения молекул и распределение молекул по скоростям. Отклонениями от закона Максвелла объясняется направленный перенос физических характеристик вещества в явлениях переноса.
Будем рассматривать только одномерные явления, при которых физические величины, определяющие эти явления, зависят только от одной координаты
1. Теплопроводность.
Явление теплопроводности наблюдается, если в различных частях рассматриваемого газа температуры различны. Рассмотрение явления теплопроводности с микроскопической точки зрения показывает, что количество теплоты переносимое через площадку ΔS, перпендикулярную направлению переноса прямо пропорционально коэффициенту тепло проводимости χ, зависящему от рода вещества или газа, градиенту температуры  , величины площадки ΔS и времени наблюдения Δt
, величины площадки ΔS и времени наблюдения Δt
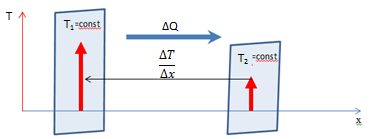
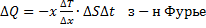
Знак минус в законе Фурье показывает, что теплота переносится в направлении убывания температуры Т.
С молекулярно-кинетической точки зрения явления теплопроводности объясняется следующим образом. В той области объёма газа, где температура выше, кинетическая энергия хаотического теплового движения молекул больше, чем в той области, где температура ниже. В результате хаотического теплового движения молекулы переходят из области, где Т выше в область, где Т меньше. При этом они переносят с собой кинетическую энергию большую, той средней кинетической энергии, которой обладают молекулы в области с меньшей энергией. Вследствие постоянных столкновений молекул с течением времени происходит процесс выравнивания средних кинетических энергий, то есть выравнивание температур.
Коэффициент теплопроводности χ равен
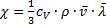

где  удельная теплоёмкость газа при постоянном объёме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объёме).
удельная теплоёмкость газа при постоянном объёме (количество теплоты, необходимое для нагревания 1 кг газа на 1 К при постоянном объёме).
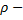 плотность газа,
плотность газа, 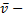 средняя скорость теплового движения молекул
средняя скорость теплового движения молекул
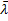
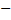 средняя длина свободного пробега.
средняя длина свободного пробега.
Физический смысл χ: коэффициент теплопроводности χ численно равен плотности теплового потока 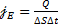 при градиенте температур
при градиенте температур  равном 1
равном 1
Диффузия
Явление диффузии заключается в самопроизвольном перемешивании молекул различных газов или жидкостей. Явление диффузии наблюдается в твердых телах. В тех случаях, когда в химически чистом однородном газе концентрация молекул будет различной, наблюдается перенос молекул, приводящей к выравниванию плотностей (или концентраций) молекул. Это явление самодиффузии. Будем для простоты считать, что плотность неоднородна вдоль оси х.
Рассмотрение явления самодиффузии с макроскопической точки зрения было сделано Фиком, который установил следующий закон: масса газа, переносимая через площадку ΔS, перпендикулярную к направлению переноса за время Δt прямо пропорциональна коэффициенту самодиффузииD, зависящему от рода газа, градиенту плотности  , величине площадки ΔS и времени наблюдения Δt.
, величине площадки ΔS и времени наблюдения Δt.
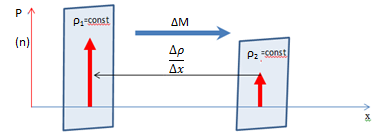
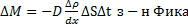
Знак минус показывает, что масса газа переносится в направлении убывания плотности. Коэффициент самодиффузии D численно равен массе газа переносимой за единицу времени через единичную площадку перпендикулярную направлению переноса, при градиенте плотности равном единице

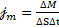 — плотность потока
— плотность потока
Согласно кинетической теории газов
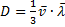
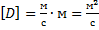
Дата добавления: 2016-01-30; просмотров: 1005;
