Движения свободного твёрдого тела
 Сферическим движением твёрдого тела называется такое движение, при котором одна точка тела остается неподвижной.
Сферическим движением твёрдого тела называется такое движение, при котором одна точка тела остается неподвижной.
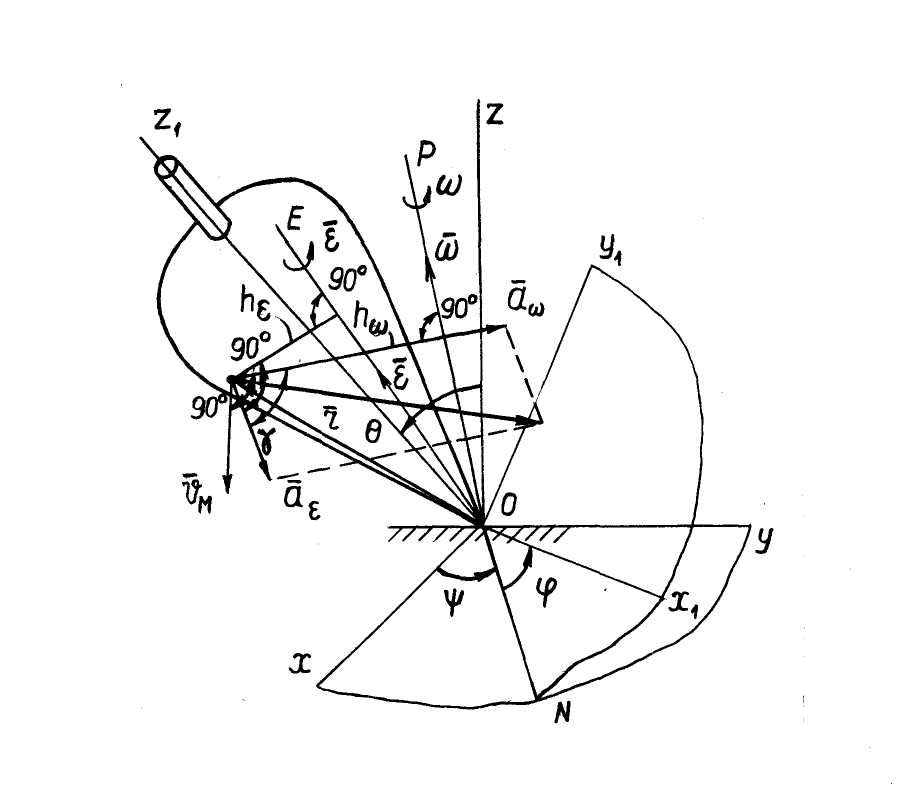
Сферическое движение совершает, например, волчок (рис. 32), у которого остаётся неподвижной точка  .
.
| Рис. 32 |
Поскольку для любой точки
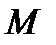 тела, совершающего сферическое движение,
тела, совершающего сферическое движение, 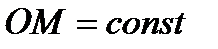 (так как тело абсолютно твёрдое), то все точки тела движутся по сферическим поверхностям с центром в точке
(так как тело абсолютно твёрдое), то все точки тела движутся по сферическим поверхностям с центром в точке  и такое движение называется сферическим.
и такое движение называется сферическим.
Для изучения сферического движения вводится неподвижная система отсчета 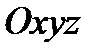 и подвижная система
и подвижная система 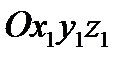 , которая движется вместе с телом.
, которая движется вместе с телом.
Линия 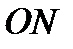 пересечения неподвижной плоскости
пересечения неподвижной плоскости 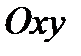 с подвижной
с подвижной 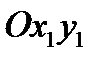 называется линией узлов.
называется линией узлов.
Для задания положения тела при сферическом движении служат углы Эйлера:
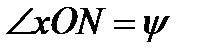 – угол прецессии;
– угол прецессии;
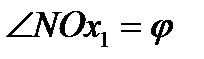 – угол собственного вращения;
– угол собственного вращения;
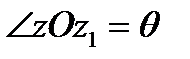 – угол нутации.
– угол нутации.
Названия указанных углов взяты из астрономии.
Выражения
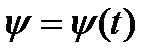 ,
, 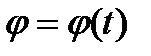 ,
, 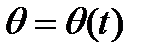 (2.31)
(2.31)
называются уравнениями сферического движения твёрдого тела.
Из теоремы Эйлера-Даламбера о перемещении твёрдого тела, имеющего одну неподвижную точку, следует, что сферическое движение в каждый момент времени можно рассматривать как мгновенное вращательное движение вокруг мгновенной оси 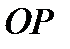 , проходящей через неподвижную точку
, проходящей через неподвижную точку  с угловой скоростью
с угловой скоростью 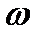 . Вектор угловой скорости
. Вектор угловой скорости 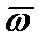 направляется по мгновенной оси
направляется по мгновенной оси 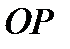 , и его направление можно определить по правилу правого винта.
, и его направление можно определить по правилу правого винта.
Поскольку для радиус-вектора 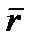 любой точки
любой точки 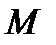 тела его модуль
тела его модуль 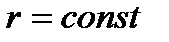 , скорости точек тела при сферическом движении можно определять по формуле Эйлера
, скорости точек тела при сферическом движении можно определять по формуле Эйлера
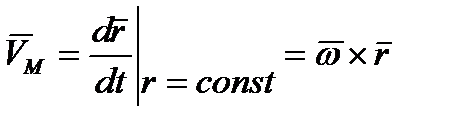 . (2.32)
. (2.32)
Векторное выражение (2.32) определяет модуль и направление вектора скорости 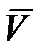 . Модуль равен
. Модуль равен
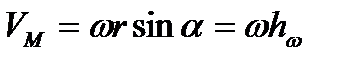 ,
,
где 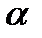 – наименьший угол между радиус-векторами
– наименьший угол между радиус-векторами 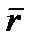 и
и 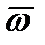 ,
, 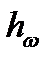 – перпендикуляр, опущенный из точки М на ось ОР.
– перпендикуляр, опущенный из точки М на ось ОР.
Из выражения (2.32) следует, что вектор скорости 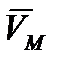 направляется перпендикулярно плоскости МОР (значит, перпендикулярно
направляется перпендикулярно плоскости МОР (значит, перпендикулярно 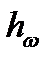 ) в сторону круговой стрелки
) в сторону круговой стрелки 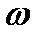 .
.
Представим векторное произведение (2.32) в виде определителя
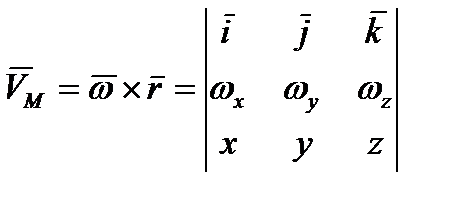 , (2.33)
, (2.33)
где 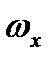 ,
, 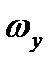 ,
,  и
и 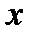 ,
, 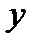 ,
, 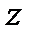 – соответственно проекции векторов
– соответственно проекции векторов 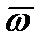 и
и 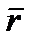 на неподвижную систему осей
на неподвижную систему осей 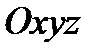 .
.
Раскладывая определитель (2.33) по элементам верхней строки, получим выражения для проекций вектора скорости 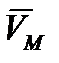 на неподвижные оси:
на неподвижные оси:
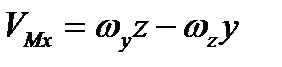 ,
, 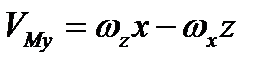 ,
, 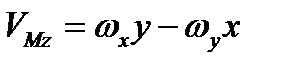 . (2.34)
. (2.34)
При сферическом движении твёрдого тела в общем случае направления векторов углового ускорения 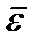 и угловой скорости
и угловой скорости 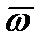 не совпадают. Вектор
не совпадают. Вектор 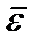 направлен по некоторой оси ОЕ, положение которой определяется в каждом конкретном случае сферического движения.
направлен по некоторой оси ОЕ, положение которой определяется в каждом конкретном случае сферического движения.
Ускорение точки тела при сферическом движении определяется путём дифференцирования по времени векторного выражения (2.32)
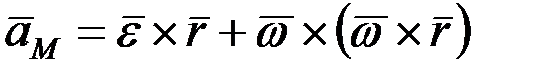 . (2.35)
. (2.35)
В выражении (2.35)
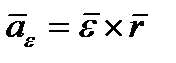 (2.36)
(2.36)
есть вращательное ускорение точки М тела. Из выражения (2.36) следует, что
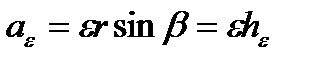 ,
,
где 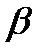 – угол наименьший между радиус-векторами
– угол наименьший между радиус-векторами 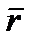 и
и 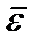 ,
, 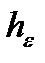 – перпендикуляр, опущенный из точки М на ось ОЕ.
– перпендикуляр, опущенный из точки М на ось ОЕ.
Вектор 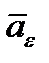 направлен перпендикулярно плоскости МОЕ (значит, перпендикулярно
направлен перпендикулярно плоскости МОЕ (значит, перпендикулярно 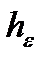 ) в сторону круговой стрелки
) в сторону круговой стрелки 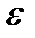 .
.
Вторая составляющая ускорения в выражении (2.35)
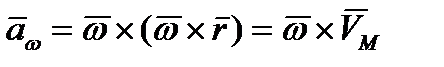 (2.37)
(2.37)
есть осестремительное ускорение точки 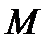 . Из выражения (2.37) следует, что
. Из выражения (2.37) следует, что
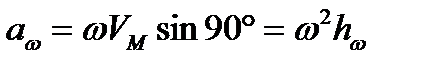
и вектор 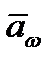 направлен по
направлен по 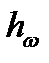 к оси ОР.
к оси ОР.
С учётом выражений (2.26) и (2.37) выражение (2.35) принимает вид
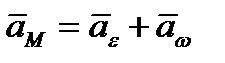 . (2.38)
. (2.38)
Равенство (2.38) выражает теорему Ривальса об ускорении точки тела, совершающего сферическое движение: ускорение любой точки тела при сферическом движении равно геометрической сумме её вращательного и осестремительного ускорений.
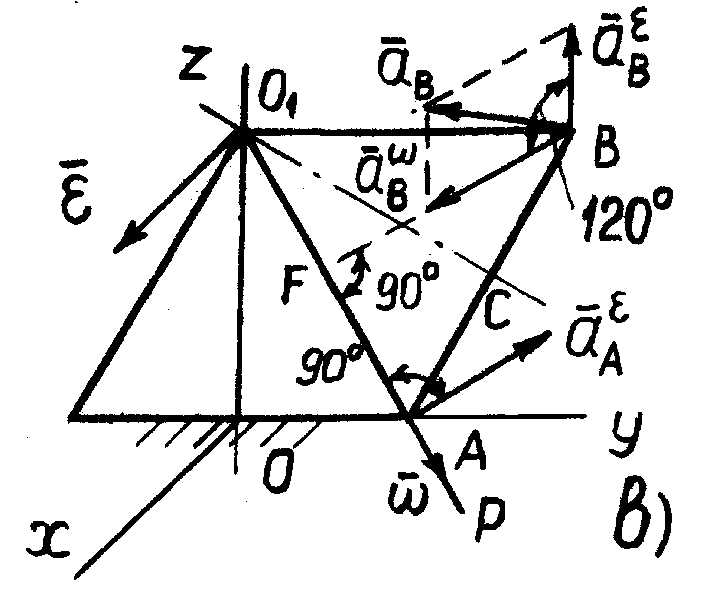
На рис. 32 ускорение 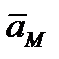 направлено по диагонали параллелограмма, построенного на векторах
направлено по диагонали параллелограмма, построенного на векторах 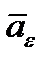 и
и 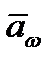 . Так как угол
. Так как угол 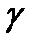 между
между 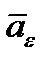 и
и 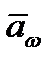 в общем случае не равен
в общем случае не равен 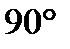 , то модуль вектора
, то модуль вектора 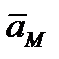 можно определить по теореме косинусов
можно определить по теореме косинусов
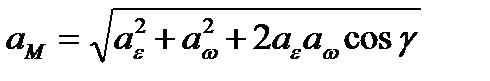 . (2.39)
. (2.39)
| Рис. 33 |
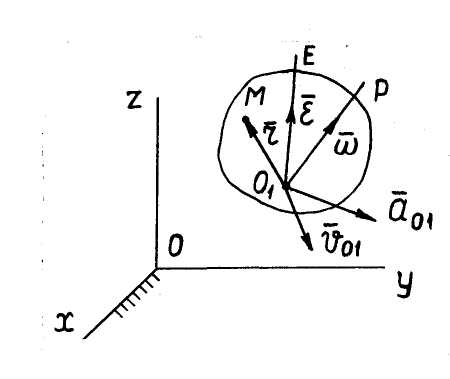 Движение свободного твёрдого тела в общем случае (рис. 33)можно представить как совокупность двух движений: поступательного вместе с некоторым полюсом
Движение свободного твёрдого тела в общем случае (рис. 33)можно представить как совокупность двух движений: поступательного вместе с некоторым полюсом 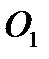 и сферического относительно полюса
и сферического относительно полюса 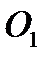 . На рис. 33 показаны
. На рис. 33 показаны  ,
, 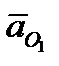 – соответственно скорость и ускорение полюса;
– соответственно скорость и ускорение полюса; 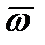 и
и 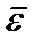 – векторы угловой скорости и углового ускорения сферического движения. В качестве полюса может быть выбрана любая точка тела.
– векторы угловой скорости и углового ускорения сферического движения. В качестве полюса может быть выбрана любая точка тела.
С учётом сказанного для свободного тела в общем случае скорость 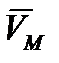 и ускорение
и ускорение 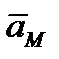 некоторой точки
некоторой точки 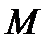 , положение которой относительно полюса
, положение которой относительно полюса 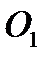 определяется радиус-вектором
определяется радиус-вектором 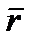 , будут равны геометрическим суммам скоростей и ускорений от поступательного и сферического движений
, будут равны геометрическим суммам скоростей и ускорений от поступательного и сферического движений
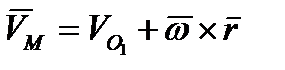 , (2.40)
, (2.40)
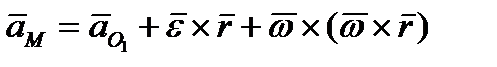 . (2.41)
. (2.41)
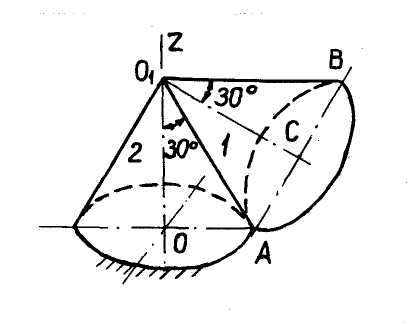
Пример 1. Конус 1 (рис. 34а) с углом при вершине 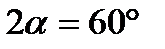 и радиусом основания AC = 0,3 м катится без скольжения по такому же неподвижному конусу 2, совершая вокруг вертикальной оси
и радиусом основания AC = 0,3 м катится без скольжения по такому же неподвижному конусу 2, совершая вокруг вертикальной оси 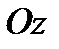
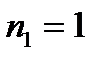 оборот за каждую секунду. Определить:
оборот за каждую секунду. Определить:
1) угловую скорость конуса 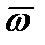 ;
;
2) угловое ускорение конуса 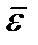 ;
;
3) скорости низшей и высшей точек основания  и
и 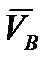 ;
;
| а) |
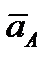 и
и 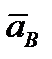 .
.
| в) |
| б) |
| Рис. 34 |
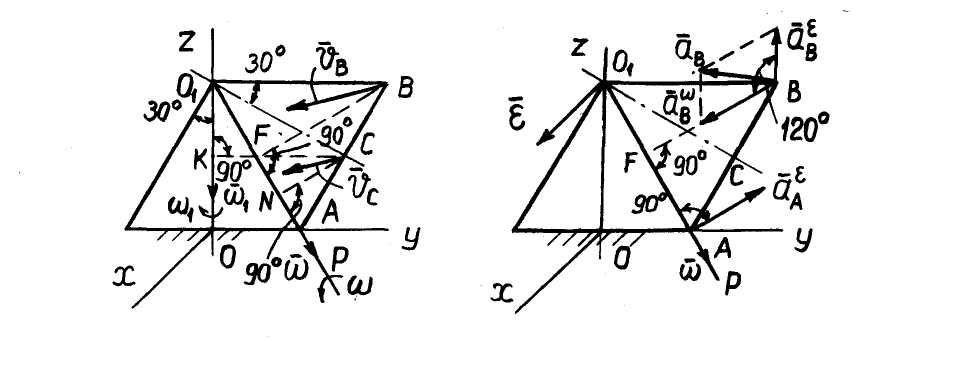 Конус 1 движется так, что его вершина
Конус 1 движется так, что его вершина 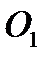 остается неподвижной, т.е. совершает сферическое движение. С другой стороны, движение конуса 1 можно рассматривать как результирующее движение от сложения вращений вокруг пересекающихся осей
остается неподвижной, т.е. совершает сферическое движение. С другой стороны, движение конуса 1 можно рассматривать как результирующее движение от сложения вращений вокруг пересекающихся осей 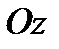 с угловой скоростью (рис. 34б)
с угловой скоростью (рис. 34б)
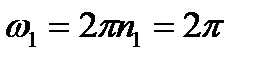 рад/с
рад/с
и оси 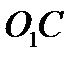 с угловой скоростью
с угловой скоростью 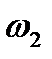 . Поскольку для точки
. Поскольку для точки 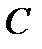 её скорость от вращения вокруг оси
её скорость от вращения вокруг оси 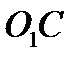 равна нулю, то
равна нулю, то
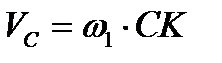 ,
,
где 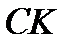 – перпендикуляр, опущенный из точки
– перпендикуляр, опущенный из точки 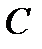 на ось
на ось 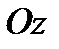 .
.
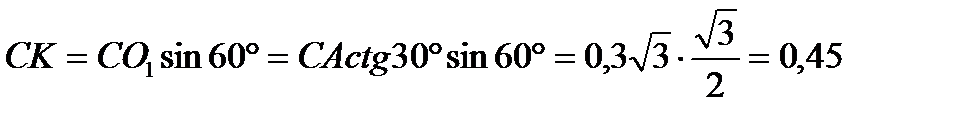 м.
м.
Значит,
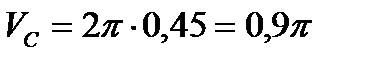 м/с.
м/с.
Вектор 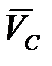 направлен перпендикулярно плоскости чертежа в сторону круговой стрелки
направлен перпендикулярно плоскости чертежа в сторону круговой стрелки 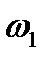 , т.е. на нас.
, т.е. на нас.
Согласно теореме Эйлера-Даламбера, сферическое движение можно рассматривать как вращательное движение с угловой скоростью 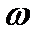 вокруг мгновенной оси
вокруг мгновенной оси 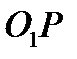 , которая совпадает с образующей
, которая совпадает с образующей 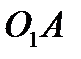 конусов 1 и 2, поскольку конус 1 катится без скольжения.
конусов 1 и 2, поскольку конус 1 катится без скольжения.
Следовательно,
 ,
,
где 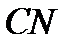 – перпендикуляр, опущенный из точки
– перпендикуляр, опущенный из точки 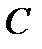 на мгновенную ось
на мгновенную ось 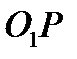 :
:
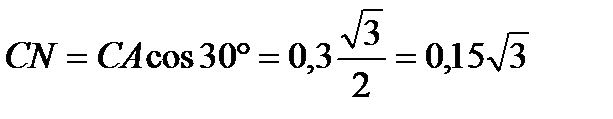 м.
м.
Следовательно, мгновенная угловая скорость
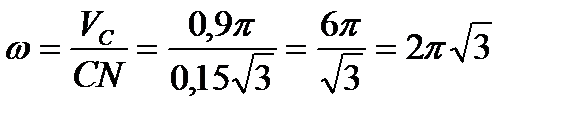 рад/с.
рад/с.
Зная направление вектора 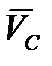 , находим направление
, находим направление 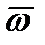 . Изображаем
. Изображаем 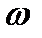 в виде вектора
в виде вектора 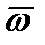 , используя правило правого винта.
, используя правило правого винта.
Так как точка 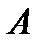 конуса 1 лежит на мгновенной оси
конуса 1 лежит на мгновенной оси 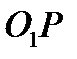 , то скорость
, то скорость
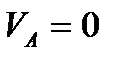 .
.
Скорость точки 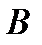
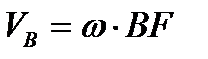 ,
,
где 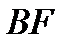 – перпендикуляр, опущенный из точки
– перпендикуляр, опущенный из точки 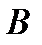 на мгновенную ось
на мгновенную ось 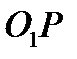 :
:
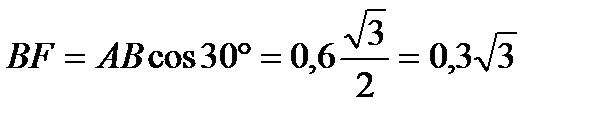 м.
м.
Следовательно,
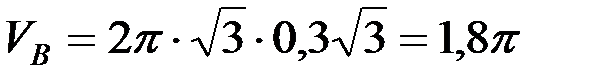 м/с.
м/с.
Вектор 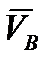 направлен на нас.
направлен на нас.
Вектор углового ускорения
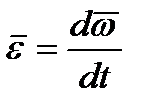 . (2.42)
. (2.42)
Так как модуль вектора 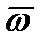 постоянный, т.е.
постоянный, т.е. 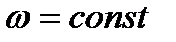 , то производную (3.42) можно определить по формуле Эйлера:
, то производную (3.42) можно определить по формуле Эйлера:
 , (2.43)
, (2.43)
где 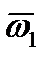 – вектор угловой скорости
– вектор угловой скорости 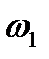 , направленный по оси
, направленный по оси 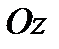 вниз.
вниз.
Из выражения (2.42) следует, что вектор углового ускорения 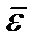 по модулю и направлению совпадает со скоростью конца вектора
по модулю и направлению совпадает со скоростью конца вектора 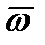 , который вращается с угловой скоростью
, который вращается с угловой скоростью 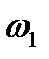 вокруг оси
вокруг оси 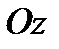 .
.
Дата добавления: 2016-01-03; просмотров: 1407;
