Законы идеального газа. Аннотация: традиционное изложение темы, дополненное демонстрацией на компьютерной модели.

Аннотация: традиционное изложение темы, дополненное демонстрацией на компьютерной модели.

Из трех агрегатных состояний вещества наиболее простым является газообразное состояние. В газах силы, действующие между молекулами, малы и при определенных условиях ими можно пренебречь.

Газ называется идеальным, если:

- можно пренебречь размерами молекул, т.е. можно считать молекулы материальными точками;

- можно пренебречь силами взаимодействия между молекулами (потенциальная энергия взаимодействия молекул много меньше их кинетической энергии);

- удары молекул друг с другом и со стенками сосуда можно считать абсолютно упругими.

Реальные газы близки по свойствам к идеальному при:

- условиях, близких к нормальным условиям (t = 0⁰C, p = 1.03·10⁵ Па);

- при высоких температурах.

Законы, которым подчиняется поведение идеальных газов, были открыты опытным путем достаточно давно. Так, закон Бойля - Мариотта установлен еще в 17 веке. Дадим формулировки этих законов.

Закон Бойля - Мариотта. Пусть газ находится в условиях, когда его температура поддерживается постоянной (такие условия называются изотермическими).Тогда для данной массы газа произведение давления на объем есть величина постоянная:

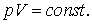
Эту формулу называют уравнением изотермы. Графически зависимость p от V для различных температур изображена на рисунке.

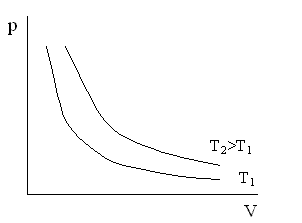
Свойство тела изменять давление при изменении объема называется сжимаемостью. Если изменение объема происходит при T=const, то сжимаемость характеризуетсяизотермическим коэффициентом сжимаемости 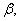который определяется как относительное изменение объема, вызывающее изменение давления на единицу.

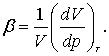
Для идеального газа легко вычислить его значение. Из уравнения изотермы получаем:

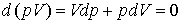
и тогда

Знак минус указывает на то, что при увеличении объема давление уменьшается. Т.о., изотермический коэффициент сжимаемости идеального газа равен обратной величине его давления. С ростом давления он уменьшается, т.к. чем больше давление, тем меньше у газа возможностей для дальнейшего сжатия.

Закон Гей - Люссака. Пусть газ находится в условиях, когда постоянным поддерживается его давление (такие условия называются изобарическими). Их можно осуществить, если поместить газ в цилиндр, закрытый подвижным поршнем. Тогда изменение температуры газа приведет к перемещению поршня и изменению объема. Давление же газа останется постоянным. При этом для данной массы газа его объем будет пропорционален температуре:

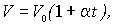
где V₀ - объем при температуре t = 0⁰C, 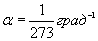- коэффициент объемного расширения газов. Его можно представить в виде, аналогичном коэффициенту сжимаемости:

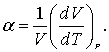
Графически зависимость V от T для различных давлений изображена на рисунке.

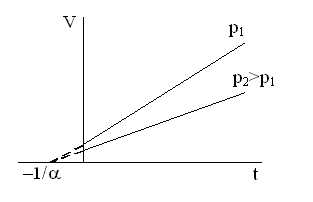
Перейдя от температуры в шкале Цельсия к абсолютной температуре 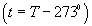, закон Гей - Люссака можно записать в виде:

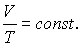
Закон Шарля. Если газ находится в условиях, когда постоянным остается его объем (изохорические условия), то для данной массы газа давление будет пропорционально температуре:

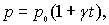
где р₀ - давление при температуре t = 0⁰C, 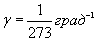- коэффициент давления. Он показывает относительное увеличение давления газа при нагревании его на 1⁰:

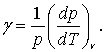
Закон Шарля также можно записать в виде:

Закон Авогадро: один моль любого идеального газа при одинаковых температуре и давлении занимает одинаковый объем. При нормальных условиях (t = 0⁰C, p = 1.03·10⁵ Па) этот объем равен 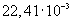м^-3/моль.

Число частиц, содержащихся в 1 моле различных веществ, наз. постоянная Авогадро:

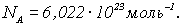
Легко вычислить и число n₀ частиц в 1 м³ при нормальных условиях:

Это число называется числом Лошмидта.

Закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов, т.е.

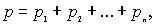
где 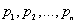- парциальные давления - давления, которые бы оказывали компоненты смеси, если бы каждый из них занимал объем, равный объему смеси при той же температуре.

Уравнение Клапейрона - Менделеева. Из законов идеального газа можно получить уравнение состояния, связывающее Т, р и V идеального газа в состоянии равновесия. Это уравнение впервые было получено французским физиком и инженером Б. Клапейроном и российским учеными Д.И. Менделеевым, поэтому носит их имя.

Пусть некоторая масса газа занимает объем V₁, имеет давление p₁ и находится при температуре Т₁. Эта же масса газа в другом состоянии характеризуется параметрами V₂, p₂, Т₂ (см. рисунок). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: изотермического (1 - 1') и изохорического (1' - 2).

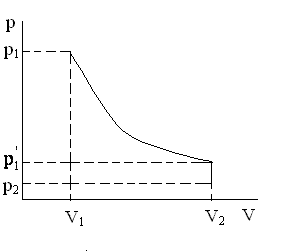
Для данных процессов можно записать законы Бойля - Мариотта и Гей - Люссака:

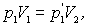
Исключив из уравнений p₁^', получим

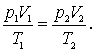
Так как состояния 1 и 2 были выбраны произвольно, то последнее уравнение можно записать в виде:

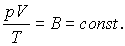
Это уравнение называется уравнением Клапейрона, в котором В - постоянная, различная для различных масс газов.

Менделеев объединил уравнение Клапейрона с законом Авогадро. Согласно закону Авогадро, 1 моль любого идеального газа при одинаковых p и T занимает один и тот же объем V_m, поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется универсальной газовой постоянной. Тогда

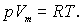
Это уравнение и является уравнением состояния идеального газа, которое также носит название уравнение Клапейрона - Менделеева.

Числовое значение универсальной газовой постоянной можно определить, подставив в уравнение Клапейрона - Менделеева значения p, T и V_m при нормальных условиях:

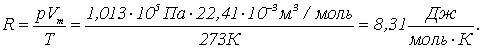
Уравнение Клапейрона - Менделеева можно записать для любой массы газа. Для этого вспомним, что объем газа массы m связан с объемом одного моля формулой V=(m/M)V_m, где М - молярная масса газа. Тогда уравнение Клапейрона - Менделеева для газа массой m будет иметь вид:

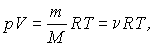
где 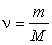- число молей.

Часто уравнение состояния идеального газа записывают через постоянную Больцмана:

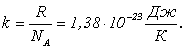
Исходя из этого, уравнение состояния можно представить как

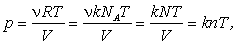
где 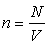- концентрация молекул. Из последнего уравнения видно, что давление идеального газа прямо пропорционально его температуре и концентрации молекул.