Внутренняя энергия тела и идеального газа

Важной характеристикой термодинамической системы является ее внутренняя энергия. Внутренней энергией системы называется энергия хаотического (теплового) движения микрочастиц и энергия их взаимодействия. Внутренняя энергия системы – однозначная функция термодинамического состояния системы: в каждом состоянии система обладает вполне определенной внутренней энергией, не зависящей от процесса, в результате которого система пришла в это состояние.

В идеальных газах отсутствует взаимодействие между молекулами, поэтому внутренняя энергия идеального газа равна сумме кинетических энергий движения всех его молекул. Как уже отмечалось, при большом числе частиц можно воспользоваться усредненными характеристиками и представить внутреннюю энергию идеального газа как произведение средней кинетической энергии ε₀ на число частиц N:

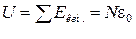(2.4.2)

Одним из основных законов классической статистической физики является закон Больцмана, согласно которому на каждую поступательную и вращательную степень свободы молекулы приходится одинаковая кинетическая энергия, равная ½ kT. На каждую колебательную степень свободы приходится одинаковое количество энергии, равное kT. Таким образом, средняя кинетическая энергия молекул по классическим представлениям пропорциональна абсолютной температуре T:

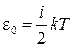. (2.4.3)

Напомним, что числом степеней свободы называется количество независимых переменных, полностью определяющих положение системы в пространстве. Молекулу одноатомного газа можно рассматривать как материальную точку, имеющую три степени свободы поступательного движения. Молекулу двухатомного газа в классической физике представляют как систему двух материальных точек, жестко связанных недеформируемой связью. Такая молекула имеет три степени свободы поступательного движения и две степени свободы вращательного движения. Вращение вокруг третьей оси, проходящей через оба атома, лишено смысла (кинетическая энергия такого вращения равна 0). Трехатомные и многоатомные молекулы имеют шесть степеней свободы: три степени свободы поступательного движения и три вращательного. Колебательными степенями свободы в модели идеального газа пренебрегают.

Таким образом, общее число степеней свободы любой молекулы

i= i_пост.+i_вр. (2.4.4)

Используя (2.4.3) и формулы молекулярно-кинетической теории, можно получить выражение для внутренней энергии идеального газа:

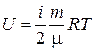. (2.4.5)

Еще раз подчеркнем, что внутренняя энергия является однозначной функцией состояния; изменение внутренней энергии в цикле равно нулю.