Геометрические элементы

Геометрически у волны выделяют следующие элементы:

· гребень волны — множество точек волны с максимальным положительным отклонением от состояния равновесия;

· долина (ложбина) волны — множество точек волны с наибольшим отрицательным отклонением от состояния равновесия;

· волновая поверхность — множество точек, имеющих в некий фиксированный момент времени одинаковую фазу колебаний. В зависимости от формы фронта волны выделяют плоские, сферические, эллиптические и другие волны.

Терминология гребня и ложбины волны, как правило, применима к поверхностным волнам на границе двух сред – например, для поверхностных волн на воде. Иногда эту терминологию используют для описания графиков волнового процесса. Для продольных волн используются понятия экстремальных точек волны: точек максимального сжатия и максимального разрежения. При этом в случае механических волн соответствующие элементарные объёмы смещаются из своих положений равновесия к области максимального сжатия или от области максимального разрежения с обеих сторон от волновых поверхностей, проходящих через экстремальные точки волны. Максимума же или минимума достигают только параметры субстанции – например, давление в элементарном объёме, концентрация определённого химического вещества, напряжённость поля, плотность элементов дискретной динамической системы и т. д.

Для стоячих волн используют понятие пучность и узел.

Временна́я и пространственная периодичности

Поскольку волновые процессы обусловлены совместным колебанием элементов динамической системы (осцилляторов, элементарных объёмов), они обладают как свойствами колебаний своих элементов, так и свойствами совокупности этих колебаний.
К первым относится временная периодичность — скорость изменения фазы с течением времени в какой-то заданной точке, называемую частотой волны ;
К волновым свойствам относится пространственная периодичность — скорость изменения фазы (запаздывание процесса во времени) в определённый момент времени с изменением координаты — длина волны λ.

Временная и пространственная периодичности взаимосвязаны. В упрощённом виде для линейных волн эта зависимость имеет следующий вид:

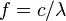
где c — скорость распространения волны в данной среде.

Для сложных процессов с дисперсией и нелинейностью, данная зависимость применима для каждой частоты спектра, в который может быть разложен любой волновой процесс.