Теорема о сложении ускорений плоской фигуры
Теорема: Ускорение любой точки М плоской фигуры геометрически складывается из ускорения какой-либо другой точки плоской фигуры (А) принятой за полюс и ускорения, которое получает эта точка (М) при вращении фигуры вокруг полюса (А).
.
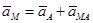Так как ускорение вращения точки может быть представлено как сумма касательного и нормального ускорений, то имеем:
.
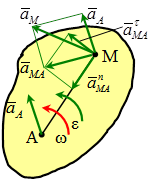
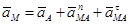Вектор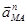 
направлен всегда от точки М к полюсу А; вектор 
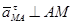и направлен в сторону «указанную» угловым ускорением ε.
Векторное уравнение может быть решено аналитически, для чего его необходимо спроецировать на координатные оси, или графически с помощью построения плана ускорений.
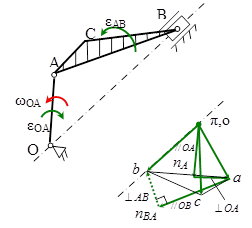
Планом ускорений называется векторная диаграмма, построенная на основе теоремы сложения ускорений. Покажем порядок построения плана ускорений для кривошипно-ползунного механизма.
Пусть заданы: положение механизма, длины звеньев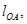 
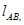
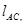
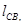
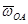и 
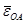. Так как точка А механизма вращается по окружности радиуса 
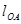, то
; 
.
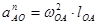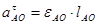Сложим эти вектора, предварительно выбрав масштабный коэффициент,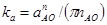 
и определив их «чертежные» длины. Конец суммарного вектора 
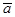обозначим буквой a. Так как шатун АВ совершает плоское движение, применим к нему теорему сложения ускорений, приняв за полюс точку А, ускорение которой уже известно:
.
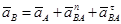Рассчитаем модуль и «чертежную» длину вектора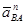 
:
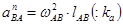, где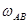 
должно быть определено ранее аналитически или графически. Отложим этот вектор от точки плана а//АВ (направление на шатуне АВ - от В к полюсу А), конец вектора обозначим 
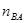. Из точки 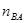проведем пунктирную прямую 
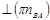до пересечения с прямой проведенной из полюса плана ускорений π //OB. Пересечение этих прямых обозначим b.
; 
.
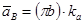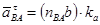Чтобы определить на плане положение точки с, соединим точки а и b отрезком прямой и построим сходственно расположенный Δabc~ΔABC на шатуне АВ (правило подобия). Направим стрелку от полюса плана π к точке с .
.
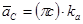Дата добавления: 2016-01-29; просмотров: 1057;