Сложное движение точки (тела)
 8.2.1 В ряде случаев целесообразно рассматривать движение точки или тела одновременно по отношению к двум системам отсчета.
8.2.1 В ряде случаев целесообразно рассматривать движение точки или тела одновременно по отношению к двум системам отсчета.
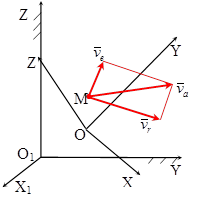
Рассмотрим неподвижную систему координат OX1 Y1 Z1 и систему OXYZ, которая движется относительно неподвижной системы. Движение точки М по отношению к неподвижной системе координат называется абсолютным или сложным движением.
Движение точки М по отношению к подвижной системе координат называется относительным движением. Движение подвижной системы координат относительно неподвижной называется переносным.
Теорема о сложении скоростей: При сложном движении абсолютная скорость точки (тела) 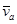 равна геометрической сумме относительной
равна геометрической сумме относительной 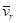 и переносной
и переносной 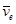 скоростей:
скоростей:
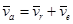 ;
;
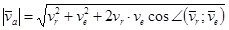 ;
;
8.2.2 Теорема о сложении ускорений: При сложном движении ускорение точки (тела) равно геометрической сумме трех ускорений: относительного 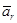 , переносного
, переносного 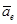 и Кориолиса
и Кориолиса 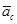 (поворотного):
(поворотного):
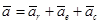 ;
;
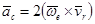 ;
;
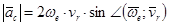 ,
,
где 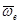 - вектор угловой скорости переносного движения.
- вектор угловой скорости переносного движения.
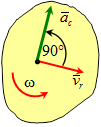
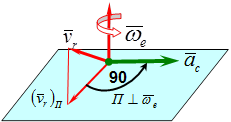 Направление ускорения Кориолиса определяют по правилу Жуковского: Вектор относительной скорости
Направление ускорения Кориолиса определяют по правилу Жуковского: Вектор относительной скорости 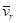 проецируется на плоскость перпендикулярную оси переносного вращения
проецируется на плоскость перпендикулярную оси переносного вращения 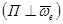 , затем вектор проекции
, затем вектор проекции 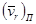 поворачивается на 900 в сторону этого вращения.
поворачивается на 900 в сторону этого вращения.
При плоском движении достаточно вектор относительной скорости 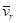 повернуть на 90° в направлении переносного вращения ωe.
повернуть на 90° в направлении переносного вращения ωe.
Ускорение Кориолиса равно нулю, если:
ü переносное движение поступательное (wе=0);
ü отсутствует относительное движение (vr=0);
ü векторы 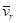 и
и 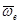 параллельны.
параллельны.
Дата добавления: 2016-01-29; просмотров: 896;
