Момент силы относительно центра (точки). Теорема Вариньона
2.1.1 Момент силы относительно центра.
Моментом силы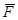 
относительно центра(точки) Оназывается вектор 
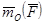равный векторному произведению радиуса вектора 
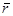, проведенного из центра О в точку А приложения силы, и вектора силы 
:
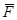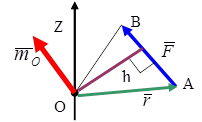
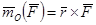
Вектор 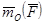приложен в точке О инаправлен ^ плоскости, проходящей через центр О и силу 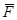, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки.
Модуль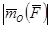 
равен произведению модуля силы 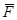на плечо h: 
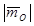= F·h,
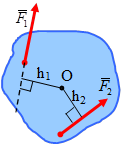где плечо h - перпендикуляр, опущенный из центра О на линию действия силы .
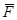Момент 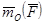характеризует вращательный эффектсилы 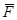относительно центра (точки) О.
Свойства момента силы:
Момент силы относительно центра не изменяется при переносе силы вдоль линии ее действия в любую точку;
Еслилиния действия силы проходит через центр О (h = 0), то момент силы относительно центра О равен нулю.
Для плоской системы сил при вычислении моментов сил относительно точки (центра), находящейся в той же плоскости, пользуются понятием алгебраического момента силы относительно точки.
Алгебраический момент силы 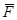относительно точки О равен взятому с соответствующим знаком произведению модуля силы на ее плечо:
mО( 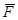) = ±F×h.
Момент считается положительным, если сила стремится повернуть тело вокруг точки О против хода часовой стрелки, и отрицательным - по ходу часовой стрелки:
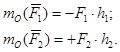
Теорема Вариньона.
При определении алгебраического момента силы относительно точки в случае, когда сложно найти плечо h, следует разложить силу на составляющие, плечи которых найти проще, (часто параллельно осям координат), и применить теорему Вариньона: если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки О равен сумме моментов составляющих сил, относительно той же точки, т. е.
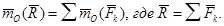Например: 
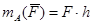, но плечо h сложно найти. Разложим силу 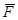на составляющие 
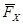и 
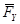, применим теорему Вариньона.
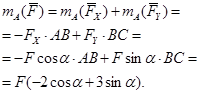
Дата добавления: 2016-01-29; просмотров: 1042;