Проекция силы на ось.

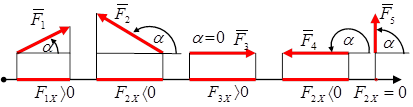
Проекцией силы на ось называется алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси:

F_X=│F│cos α;

F_X>0, если0<a<p/2;

F_X <0, если p/2<a<p;

F_X=0, если a=p/2 или α=3/2π

1.3.3 Аналитический способ задания сил на плоскости.

Силу 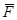можно задать через ее проекциина оси прямоугольной системы координат F_X, F_Y и F_Z по правилу сложения векторов, определив точку приложения силы:

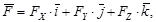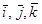где - единичные векторы. Модуль силы и углы, которые она образует с координатными осями, будут:

В пространстве:

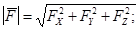
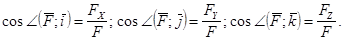
На плоскости:

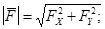
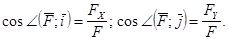
1.3.4 Аналитический способ сложения сил.

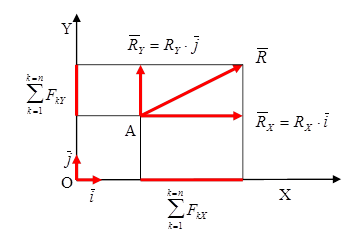
Воспользуемся теоремой: проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось. Спроецируем равенство 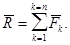на оси прямоугольной системы координат Оху, получим

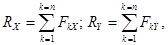
где F_k_X, F_k_Y - проекции k-ой силы 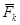на оси Ох и Оу соответственно. Тогда на плоскости Оху вектор 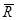определяется по формулам:

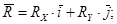
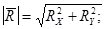
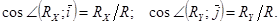
Система сходящихся сил на плоскости

Основные понятия.

Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил.

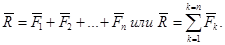Действие системы сходящихся сил 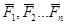на тело эквивалентно действию одной силы 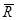, которая называется равнодействующей:

Равнодействующая 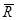приложена в точке сходимости О и является замыкающим вектором при построении силового многоугольника.

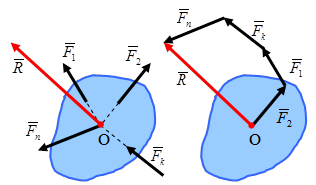
Для равновесиятвердого тела, находящегося под действием сходящейся системы сил, необходимо и достаточно, чтобы равнодействующая этих сил была равна нулю:

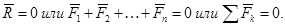
Это векторное условие равновесия сходящейся системы сил.

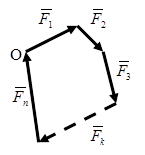Геометрическим условием равновесия твердого тела, находящегося под действием сходящейся системы сил 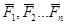является замкнутость силового многоугольника, т. е. начало первого вектора 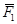должно совпадать с концом последнего .

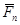Аналитические условия равновесия плоской сходящейся системы сил. При равновесии системы сил модуль равнодействующей R = (R_х² + R_у²)^1/2 = 0, что возможно, если одновременно R_х = 0, R_у = 0. Следовательно, для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на оси координат Оху были равны нулю, то есть:

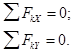
1.4.2 Теорема о трех непараллельных силах.

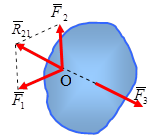Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действияэтих силпересекаются в одной точке.

Так как, 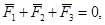то 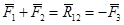. Следовательно, согласно аксиоме 1, (см. п. 1.1.2) линия действия силы 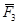пересекает точку О сходимости сил .

<123 4 5 6 7 >

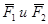Дата добавления: 2016-01-29; просмотров: 3872;