Метод двух изображений. Модель точки на эпюре Монжа. Связь между ортогональными проекциями и декартовой системой координат

МЕТОД ДВУХ ИЗОБРАЖЕНИЙ

С помощью операции проецирования можно получить проекцию любой точки пространства, но по проекции точки невозможно определить положение точки в пространстве. Действительно, точке пространства на плоскости соответствует единственная точка, но если мы попытаемся по проекции точки определить положение самой точки в пространстве, то увидим, что проекции точки соответствует все множество точек проецирующего луча. Для установления взаимно однозначного соответствия между точками пространства и их моделью используют метод двух изображений. В трехмерном пространстве выбирают две плоскости проекций и два центра проецирования. В зависимости от взаимного расположения плоскостей проекций и центров проецирования, а также в зависимости от способа перехода к одной картинной плоскости возникают различные частные варианты метода двух изображений. На практике наибольшее распространение получили следующие варианты метода двух изображений: эпюр Монжа, перспектива и аксонометрия.

Для выполнения технических чертежей особенно удобен эпюр Монжа – параллельное ортогональное проецирование на две взаимно перпендикулярные плоскости проекций (рис. 2.1.). В исходном пространстве выбираются две взаимно перпендикулярные плоскости проекций (π₁ и π₂) и два бесконечно удаленных центра проецирования (S₁ и S₂). Центр S₁ удален по направлению, перпендикулярному к π_1, а S₂ – по направлению, перпендикулярному к π₂. Линия пересечения плоскостей проекций называется осью проекций х. Плоскость проецирующих лучей α (S₁S₂А)расположена перпендикулярно к плоскостям проекций и пересекает их по прямым линиям а₁ и а₂, перпендикулярным к оси проекций х. Для перехода к одной плоскости чертежа спроецируем изображение с π₁ на π₂ из бесконечно удаленного центра R, в направлении под углом 45° к плоскостям проекций, что равносильно повороту плоскости π₁ вокруг оси х до совмещения с π₂ (рис. 2. 2). Прямые линии а₁ и α₂ на эпюре сливаются в одну линию связи между проекциями, перпендикулярные к оси проекций х. Моделью точки А на эпюре Монжа является пара точек А₁ и А₂, расположенных на линии связи. Плоскости проекций условно делят пространство на четыре четверти (квадранта).

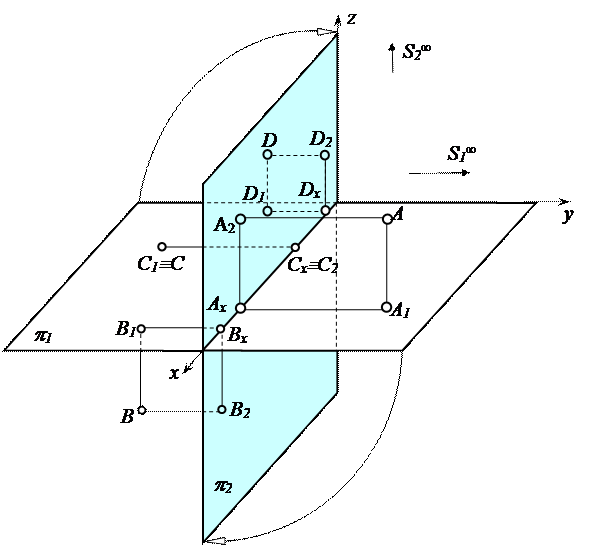Рис. 2.1. Параллельное ортогональное проецирование точек на две взаимно перпендикулярные плоскости проекций

Если точка А расположена в первой четверти пространства, то ее проекции на эпюре Монжа располагаются по обе стороны от оси проекций: А₁ расположена внизу, а А₂ – вверху. Проекции точки, расположенной во второй четверти пространства, будут лежать над осью проекций. Проекции точки В, лежащей в третьей четверти пространства, располагаются по обе стороны от оси, но В₁ лежит над осью, а В₂ – под осью. Для точки, лежащей в четвертой четверти пространства, обе проекции расположены под осью проекций. Если точка расположена во фронтальной плоскости, то на эпюре Монжа её горизонтальная проекция лежит на оси х. Если точка С расположена в горизонтальной плоскости, то ее фронтальная проекция лежит на оси проекций.

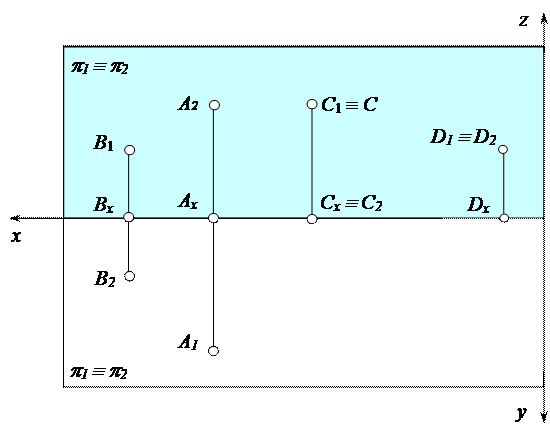
Рис. 2.2. Эпюр Монжа

В аналитической геометрии положение точки в пространстве задается тремя координатами х, у и z прямоугольной декартовой системы координат. Чтобы установить связь между ортогональными проекциями точки и ее координатами, необходимо подсоединить координатные оси к плоскостям проекций. Начало отсчета точка О выбирается на оси проекций, ось абсцисс х совпадает с осью проекций, ось ординат у располагаем в плоскости π₁, ось аппликат z – в плоскости π₂ (рис. 2.1 и 2.2). На эпюре Монжа оси ординат и аппликат совпадают между собой, но имеют разные направления и расположены перпендикулярно к оси проекций, с которой совпадает ось абсцисс (рис. 2.2). Расстояние от точки А до горизонтальной плоскости проекций равно координате Z_A и измеряется от фронтальной проекции точки А₂ до оси проекций. Расстояние от точки А до фронтальной плоскости проекций равно координате У_A и измеряется от горизонтальной проекции точки А₁ до оси проекций. Если заданы координаты точки, то всегда можно построить её проекции, и, наоборот, по проекциям точки можно определить её координаты. Рассмотрим особенности проекций точек расположенных в биссекторной плоскости τ (делящей двугранный угол пополам), проходящей через вторую и четвертую четверти пространства. Эти точки равноудалены от плоскостей проекций и их проекции на эпюре Монжа совпадают (точка D на рис. 2.1, 2.2, 2.3).

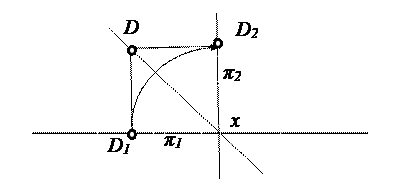
Рис. 2.3. Тождественная плоскость