Преобразования и построение дополнительного поля проекций
Известные из школьного курса геометрии плоские преобразования: перемещение или движение, осевая или центральная симметрия, сжатие или растяжение, вращение и подобие, а также растяжение или сжатие и перспективно- аффинное соответствие или родство – являются частными случаями гомологии, которая задается центром S, с осью s и парой соответственных точек А1 и А2 (рис. 2.12).
Рис. 2.12. Гомология
Гомология с бесконечно удаленным центром называется перспективно-аффинным соответствием (рис. 2.13).
Рис. 2.13. Перспективно-аффинное соответствие
Перспективно-аффинное соответствие с центром, удаленным в бесконечность перпендикулярно к оси гомологии, определяет растяжение или сжатие (рис. 2.14). Если при этом пара соответственных точек выбирается по обе стороны от оси, на равном расстоянии, то получается осевая симметрия (рис. 2.15).
Рис. 2.14. Растяжение или сжатие
Рис. 2.15. Осевая симметрия
Гомология, с бесконечно удаленной осью, определяет на плоскости преобразование подобия или гомотетию (рис. 2.16). Если при этом пара соответственных точек выбирается по обе стороны от центра на равном расстоянии, то получаем центральную симметрию (рис. 2.17).
Рис. 2.16. Подобие или гомотетия
Гомология, с бесконечно удаленным центром и бесконечно удаленной осью (элация), определяет параллельный перенос на вектор (рис. 2.18).
Рис. 2.17. Центральная симметрия
Рис. 2.18. Элация или параллельный перенос на вектор
Преобразование вращения или поворот задается центром вращения, который сам себе соответствует, радиусом вращения и углом поворота (рис. 2.19).
Так как любая точка на плоскости проекций является элементом модели точки пространства, уместно предположить, что любое преобразование на плоскости порождается преобразованием в пространстве и, наоборот, преобразование в пространстве вызывает преобразование на плоскости. Все преобразования, выполняемые в пространстве и на модели, проводятся с целью упрощения решения задач. Как правило, такие упрощения связаны с геометрическими образами частного положения и, следовательно, суть преобразований, в большинстве случаев, сводится к преобразованию образов общего положения в частное.
Рис. 2.18. Поворот или вращение
Построенная по методу двух изображений плоская модель трехмерного пространства вполне однозначно или, как говорят, изоморфно сопоставляет элементы трехмерного пространства с их моделью. Это позволяет решить на плоскостях практически любую задачу, которая может возникнуть в пространстве. Но иногда по некоторым практическим соображениям, бывает целесообразно дополнить такую модель третьим изображением объекта моделирования.
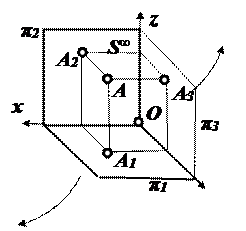
При решении позиционных и метрических задач начертательной геометрии очень часто удобна дополнительная проекция. Известные способы построения дополнительных проекций объединяются общим алгоритмом Гаука (названным по имени немецкого учёного, занимавшегося исследованием рассматриваемого вопроса). Рассмотрим частные варианты алгоритма Гаука на эпюре Монжа. Из курса черчения хорошо известна дополнительная проекция на профильную плоскость π3, перпендикулярную одновременно к плоскостям π1 и π2 (рис. 2.20). После совмещения плоскостей π1 и π3 с плоскостью π2, ось y имеет два направления, одно является продолжением оси z , а другое – оси х.
 | |||
 | |||
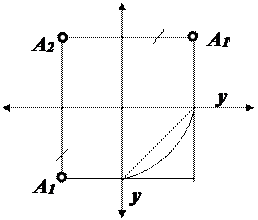Рис. 2.20. Дополнительная проекция на профильную плоскость
Интерес представляет тот случай, когда дополнительная плоскость проекций π4 перпендикулярна к одной из основных плоскостей проекций, например, к горизонтальной плоскости π1. Проецирование на π4 ортогональное из бесконечно удаленного центра S4 (рис. 2.21).
Рис. 2.21. Построение дополнительной проекции точки
Для перехода к одной картине можно плоскость π4 также как π2 повернуть вокруг оси х14 до совмещения с плоскостью π1 (рис. 2.22). Так как плоскость π4 перпендикулярна к горизонтальной плоскости проекций, то А1 и А4 будут лежать на одной линии связи, перпендикулярной к новой оси проекций х14, а расстояние от фронтальной проекции точки А2 до оси х12 (координата Z) равно расстоянию от дополнительной проекции точки А4 до оси х14. В литературе этот вариант известен как метод перемены или замены плоскостей проекций. Так как плоскость π1 и точка неизменны, т.е. расстояние от точки горизонтальной плоскости π1 неизменно, то расстояние от фронтальной проекции точки А2 до оси х12 равно расстоянию от дополнительной проекции точки А4 до оси х14.
 | |||||
| |||||
 |
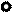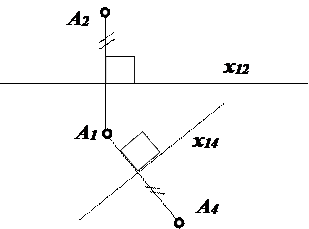Рис. 2.22. Метод перемены плоскостей проекций
В случае если π4 будет перпендикулярна к π2, никаких принципиальных различий в схеме построения дополнительной проекции не произойдет. Рассмотрим примеры решения четырех основных задач: 1 – преобразование прямой общего положения в линию уровня, 2 – преобразование прямой общего положения в проецирующее, 3 – преобразование плоскости общего положения в проецирующую плоскость и 4 – преобразование плоскости общего положения в плоскость уровня. Для решения первой задачи вводим новую плоскость π4 параллельно прямой и перпендикулярно к одной из данных плоскостей проекций. Проводим новую ось проекций, например х14, параллельно первой проекции прямой (рис. 2.23) и строим дополнительные проекции двух точек прямой по схеме, приведенной на рис. 2.22. Преобразование прямой общего положения в проецирующее положение проводится в два этапа: в начале решается первая задача, а затем вводится дополнительная плоскость π5, перпендикулярная к прямой уровня и плоскости π4 (рис. 2.23).
Для преобразования плоскости общего положения в проецирующую плоскость вводим дополнительную плоскость π4 перпендикулярно к π1 (рис 2.24) или π2; а новую ось проекций проводим, соответственно, перпендикулярно к горизонтали или фронтали плоскости. Затем строим дополнительные проекции элементов, задающих плоскость (рис 2.24). Преобразование плоскости общего положения в плоскость уровня проводится в два этапа: вначале плоскость преобразуется в проецирующую плоскость, затем вводится дополнительная плоскость π5, параллельная заданной плоскости и перпендикулярная к π4. На основе общего признака плоскостей уровня ось х45 проводится параллельно вырожденной проекции данной плоскости (рис. 2.24).
 |
Рис. 2.23. Преобразование прямой линии общего положения в линию уровня и в проецирующее положение
В качестве дополнительной плоскости проекций часто бывает удобно использовать тождественную плоскость τ. Проецирование может быть параллельным (рис. (рис 2.25)) или центральным. При этом возникает один из самых простых вариантов схемы Гаука. Построение недостающей проекции точки С, лежащей на профильной прямой АВ, соответствует известному алгоритму пропорционального деления отрезка в заданном отношении.
Рис. 2.24. Преобразование плоскости общего положения в проецирующее положение и положение уровня
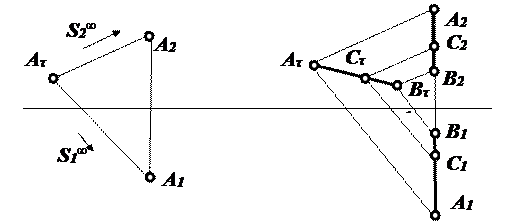
Рис. 2.25. Дополнительное проецирование на тождественную плоскость
Дополнительную плоскость проекций можно совмещать с одной из основных плоскостей проекций. Проецирование на дополнительную плоскость может быть центральным или параллельным, но не должно совпадать с направлением проецирования на основную плоскость проекций. Рассмотрим дополнительное проецирование точки А на горизонтальную плоскость проекций π1 из центра S∞ (рис. 2.26). Алгоритм построения дополнительной проекции точки следующий: из А2 проводим луч А2S2∞ до пересечения с осью х. Из полученной точки проводим линию связи, перпендикулярно к оси х, до пересечения с лучом А1S1∞. Точка пересечения построенных линий – искомая дополнительная проекция точки А.
Рис. (рис 2.26) Дополнительное проецирование точки на горизонтальную плоскость проекций
Рассмотрим вращение точки А вокруг оси i, перпендикулярной к горизонтальной плоскости проекций (рис. 2.27). Точка А при вращении описывает окружность q с центром О, лежащим на оси i.
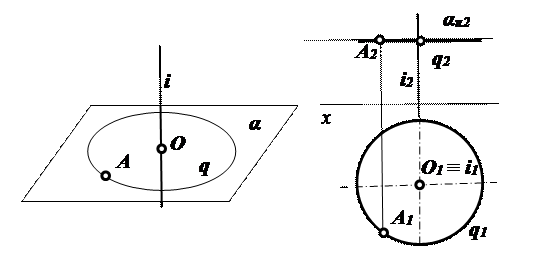
Рис. 2.27. Вращение точки вокруг оси
Плоскость окружности α перпендикулярна к оси i и параллельна плоскости проекций π1. На эпюре Монжа на горизонтальной плоскости окружность изображается в натуральную величину, а фронтальная проекция окружности q2 изображается в виде отрезка прямой линии, перпендикулярного к оси вращения и совпадающим со следом плоскости вращения απ2. При вращении какой-либо линии вокруг оси образуется произвольная поверхность вращения.
Точка А может перемещаться в плоскости α, параллельной плоскости проекций, по произвольной траектории. Если траектории перемещения точек плоской фигуры лежат в плоскостях, параллельных плоскости проекций, то проекция плоской фигуры хотя и меняет своё положение, но остается конгруэнтной, т.е. равной. Метод плоскопараллельного перемещения используют для изменения положения фигур относительно плоскостей проекций. Методом плоскопараллельного перемещения можно решать различные позиционные и метрические задачи. В частности, можно определять натуральную величину плоской фигуры. Рассмотрим пример определения натуральной величины треугольника АВС (рис. 2.28).
Рис. 2.28. Метод плоскопараллельного перемещения
Для перевода плоскости общего положения в положение уровня необходимо последовательно выполнить два перемещения параллельно плоскостям проекций. В начале переместим плоскость треугольника АВС параллельно горизонтальной плоскости проекций так, чтобы он занял фронтально проецирующее положение. В плоскости общего положения нельзя провести проецирующие прямые. Если треугольник перемещать так, чтобы его горизонталь стала фронтально проецирующей прямой, то и вся плоскость треугольника займет фронтально проецирующее положение. Для этого проведем горизонталь и расположим горизонтальную проекцию треугольника так, чтобы горизонтальная проекция горизонтали h1 была перпендикулярна к оси проекций. Перемещённое положение горизонтальной проекции треугольника строится методом засечек. В начале замерим горизонтальную проекцию горизонтали и отложим её в любом месте перпендикулярно к оси проекций. Затем замерим циркулем расстояние от точки А1 до точки В1 и сделаем засечку от А1'. Далее замерим циркулем расстояние от точки 11 до точки В1 и сделаем засечку от 11'. На пересечении засечек получим точку В1'. Аналогично построим точку С1'. Такое построение называется методом треангуляции и соответствует тому, что мы как бы вырезали горизонтальную проекцию треугольника и приклеили в другом месте. Так как траектории движения всех точек треугольника расположены в плоскостях параллельных горизонтальной плоскости проекций, то фронтальные проекции точек треугольника должны перемещаться по прямым линиям, параллельным оси проекций х, и лежать на линиях связи. Тогда фронтальная проекция горизонтали h2 будет изображаться одной точкой, а фронтальная проекция треугольника А2В2С2 – отрезком прямой линии, т.е. треугольник станет занимать проецирующее положение. Далее переместим плоскость треугольника АВС параллельно фронтальной плоскости проекций так, чтобы он занял горизонтальное положение. Для этого фронтальную проекцию треугольника А2'В2'С2' переместим так, чтобы она стала параллельна оси проекций х. Так как теперь траектории движения всех точек треугольника расположены в плоскостях параллельных фронтальной плоскости проекций, то горизонтальные проекции точек треугольника должны перемещаться по прямым линиям, параллельным оси проекций х, и лежать на линиях связи. Дополнительная проекция треугольника А1″В1″С1″, полученная в результате двойного плоскопараллельного перемещения, является натуральной величиной.
Дата добавления: 2016-01-29; просмотров: 1606;