Равновесие системы тел

Статический расчет системы тел сводится к рассмотрению условий равновесия конструкций, состоящих из не жестко соединенных между собой тел. Связи между частями конструкции называются внутренними, скрепляющие конструкцию с другими телами, - внешними.

Системы тел, для которых число неизвестных реакций связей равно числу уравнений равновесия, называются статически определимыми. Если число неизвестныхреакций связейбольше числа уравнений равновесия (на одно, два и т.д.), то системы тел называются статически неопределимыми (соответственно один, два и т.д. раза). Такие задачи невозможно решить методами статики.

При решении задач на равновесие системы тел обычно конструкцию расчленяют на отдельные тела и составляют уравнения равновесия для каждого из тел в отдельности. При этом проверяют, не превышает ли число неизвестных реакций связей число уравнений равновесия, которые можно составить для данной конструкции

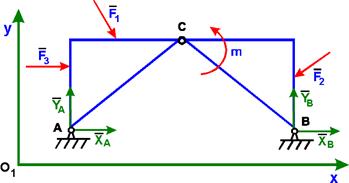
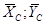Пример. Для определения внутренних и внешних реакций связей трех шарнирной аркирасчленим конструкцию по соединительному шарниру С на две части и рассмотрим равновесие каждой из частей в отдельности. Внешние реакции шарниров А и В разложим на составляющие . Реакцию со стороны части СВ на АВ разложим на составляющие , а реакцию со стороны АС на ВС на составляющие 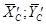. Так как по третьему закону Ньютона (аксиома 4, §1) 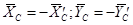, то неизвестных реакций связей в уравнения равновесия войдет шесть.

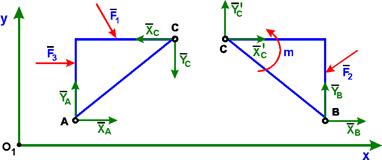
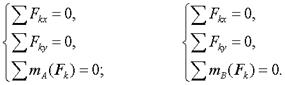
При действии на трех шарнирную арку заданной произвольной плоской системы сил для каждой части можно записать по три уравнения равновесия:

для АС для СВ

Следовательно, система тел, образующих арку, статически определима.

Для проверки решения задачи считают всю конструкцию отвердевшей (принцип отвердевания, аксиома 5, §1) и составляют одно - два уравнения равновесия для конструкции в целом или строят в масштабе многоугольник внешних активных сил и реакций связей, действующих на конструкцию. Если проверочные уравнения равновесия обращаются в тождества, а многоугольник сил замкнут, то задача решена верно.