Кінетичний момент твердого тіла відносно осі обертання
Розглянемо тверде тіло, яке обертається навколо осі Oz з кутовою швидкістю 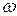 (рис.32.2).
(рис.32.2).

Рис. 33.2
Для довільної точки тіла 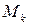 масою
масою  , яка розташована на відстані
, яка розташована на відстані 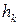 від осі обертання і має швидкість
від осі обертання і має швидкість  , кінетичний момент:
, кінетичний момент:
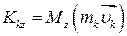 .
.
Але 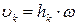 , причому вектор кількості руху точки перпендикулярний до
, причому вектор кількості руху точки перпендикулярний до 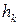 , тобто він лежить у площині, перпендикулярній до осі
, тобто він лежить у площині, перпендикулярній до осі 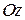 . Отже виходить, що:
. Отже виходить, що:
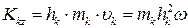 .
.
Кінетичний момент всього тіла:
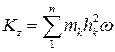 .
.
Як було визначено раніше, 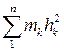 є моментом інерції тіла відносно осі
є моментом інерції тіла відносно осі 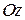 (формула 3.50), тому, кінцево:
(формула 3.50), тому, кінцево:
 . .
| (33.22) |
Таким чином, кінетичний момент твердого тіла відносно нерухомої осі обертання дорівнює добутку момента інерції тіла відносно цієї осі на кутову швидкість тіла.
Знак кінетичного момента співпадає зі знаком кутової швидкості.
Теорема моментів
З’ясуємо, як змінюється з часом вектор кінетичного момента матеріальної точки масою 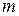 . Для цього продиференціюємо за часом вираз (33.17):
. Для цього продиференціюємо за часом вираз (33.17):
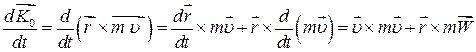 . .
|
Але 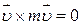 як векторний добуток двох паралельних векторів, а
як векторний добуток двох паралельних векторів, а 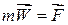 (основний закон динаміки). Отже,
(основний закон динаміки). Отже,
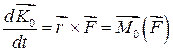 . .
| (33.23) |
Співвідношення (33.23) є математичним записом теореми про зміну момента кількості руху матеріальної точки:
похідна за часом від вектора кінетичного момента точки відносно деякого нерухомого центра О дорівнює моменту рівнодіючої сил, прикладених до точки, відносно того ж центра.
Система рівнянь
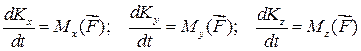 , ,
| (33.24) |
яка є висновком з (33.23), виражає теорему моментів відносно координатних осей.
Розглянемо механічну систему, що складається з 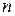 матеріальних точок. Для будь-якої
матеріальних точок. Для будь-якої 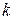 -ї точки системи теорема моментів з поділом сил, прикладених до неї, на зовнішні і внутрішні, набуває вигляду:
-ї точки системи теорема моментів з поділом сил, прикладених до неї, на зовнішні і внутрішні, набуває вигляду:
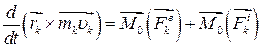 . .
|
Підсумовування по всіх точках даної системи приводить до виразу:
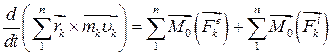 . .
|
Як відомо, 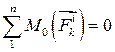 , а
, а  , тоді кінцево отримаємо:
, тоді кінцево отримаємо:
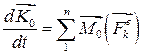 . .
| (33.25) |
Таким чином, для механічної системи похідна за часом від кінетичного момента механічної системи відносно деякого нерухомого центра О дорівнює геометричній сумі моментів зовнішніх сил, що діють на систему, відносно того ж центра.
Якщо спроектувати векторне рівняння (33.25) на осі нерухомої системи координат Оxyz, то отримаємо систему алгебраїчних рівнянь, які будуть математичним записом цієї теореми відносно відповідних координатних осей:
 . .
| (33.26) |
Теорема про зміну кінетичного момента механічної системи залишається справедливою і для випадків, коли система координат  рухається поступально разом з центром мас
рухається поступально разом з центром мас 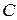 системи. Тоді:
системи. Тоді:
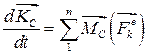 . .
| (33.27) |
В кінематиці було показано, що рух твердого тіла в загальному випадку складається із поступального руху деякої точки, яка приймається за полюс, і обертального руху навколо полюса. Якщо за полюс вибрати центр мас, то поступальна частина руху може бути досліджена за допомогою теореми про рух центра мас, а обертання навколо центра мас – за допомогою теореми моментів.
З теореми про зміну момента кількості руху системи можна отримати висновки, які виражають закон збереження кінетичного момента системи.
1. Якщо сума моментів всіх зовнішніх сил системи відносно деякого цента О дорівнює нулю, тобто 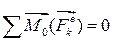 , то кінетичний момент системи відносно того ж центра є сталим за величиною і напрямом:
, то кінетичний момент системи відносно того ж центра є сталим за величиною і напрямом:
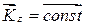 . .
|
Оскільки в цьому випадку  , отримаємо:
, отримаємо:
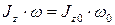 , ,
| (33.28) |
де: 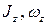 - момент інерції системи і її кутова швидкість в довільний момент часу
- момент інерції системи і її кутова швидкість в довільний момент часу 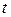 ;
;
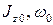 - момент інерції і кутова швидкість системи в момент часу, який прийнято за початковий
- момент інерції і кутова швидкість системи в момент часу, який прийнято за початковий 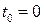 .
.
Дата добавления: 2016-01-26; просмотров: 2445;
