Диференціальні рівняння руху механічної системи

Розглянемо механічну систему, що складається з «n» матеріальних точок. Використаємо принцип звільнення від в’язей і замінимо в’язі їх реакціями. Всі сили, що діють на систему, поділимо на зовнішні і внутрішні. Тоді для довільної точки k системи масою на підставі основного закону динаміки отримаємо:

,

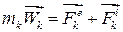(32.12)

де - рівнодіючі зовнішніх сил, які діють на 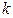- ту точку.

Аналогічного виду рівняння отримаємо і для будь-якої точки системи. Тобто всього для заданої системи будемо мати n таких рівнянь ( ).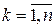

Така система рівнянь і є диференціальними рівняннями руху механічної системи у векторній формі.

Якщо спроектувати n рівнянь (32.12) на осі обраної системи координат, то отримаємо систему алгебраїчних диференціальних рівнянь руху системи в проекціях на осі.

Наприклад, при використанні декартової системи координат 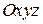будемо мати 3n скалярних рівнянь виду:

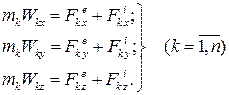
(32.13)

Як можна бачити, для визначення руху механічної системи за заданими силами і початковими умовами необхідно проінтегрувати систему з 3n диференціальних рівнянь. Цю задачу не завжди можна розв’язати точно навіть для однієї точки. Вона виключно складна у випадку двох матеріальних точок, що рухаються під дією сил взаємодії за законом всесвітнього тяжіння, і зовсім не може бути розв’язана при взаємодії трьох точок.

Інколи з диференціальних рівнянь (32.13) можна отримати так звані перші інтеграли, тобто співвідношення, до яких не входять похідні другого порядку від координат за часом. До таких перших інтегралів відносяться закони збереження механічного руху і загальні теореми динаміки системи матеріальних точок.

Завдяки впровадженню спеціальних сумарних характеристик руху всієї системи в цілому, які мають наочний фізичний зміст, загальні теореми динаміки є ефективним апаратом механіки і широко використовуються в інженерних розрахунках.

При цьому необхідно пам’ятати, що у математичні вирази цих теорем, а також до формул, що є висновками з загальних теорем, входять абсолютні швидкості і абсолютні прискорення.

Питання для самоконтролю

1. Які дві класифікації сил застосовують у динаміці? У чому їх умовність?

2. В якій механічній системі внутрішні сили знаходяться у рівновазі?

3. Декілька автомобілів рухаються по дорозі. Чи утворюють вони механічну систему?

4. Вагон, що рухається, ударяється об нерухомий вагон. На який з них буде діяти більша сила?

5. Якими величинами характеризується розподіл мас в механічній системі?

6. Як визначається центр мас механічної системи?

7. Як визначаються і як класифікуються моменти інерції механічної системи?

8. Які осі називають головними центральними осями? Які властивості вони мають?

9. Як формулюється теорема Гюйгенса?

10. Для деякого тіла радіус інерції відносно осі 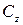, що проходить через центр мас, дорівнює 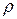. Чи є осі, які паралельні осі 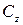, відносно яких величина радіуса інерції цього тіла буде: більше 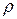? менше ?

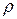Заняття 33