Обчислення кінетичного момента в деяких випадках руху твердого тіла

1. Якщо тверде тіло здійснює поступальний рух, то кінетичний момент тіла відносно деякої осі дорівнює моменту кількості руху його центра мас відносно тієї ж осі. Дійсно,

.

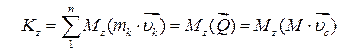(33.30)

2. Кінетичний момент твердого тіла, яке здійснює плоскопаралельний рух, відносно будь-якої осі, перпендикулярної до площини руху цього тіла, дорівнює сумі момента кількості руху центра мас тіла відносно обраної осі і момента кількості руху відносно осі, що проходить через центр мас тіла паралельно обраній.

.

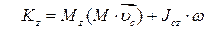(33.31)

В наведених двох останніх формулах - маса всього тіла.

Кінетична енергія і робота. Теореми про зміну кінетичної енергії

Кінетична енергія також є мірою механічного руху матеріальних об’єктів, але на відміну від кількості руху і кінетичного момента, які використовують для характеристики відповідно поступального і обертального рухів, вона існує при будь-якому русі матеріальної точки чи механічної системи.

В свою чергу, кінетична енергія тісно пов’язана з поняттям роботи сили.

Кінетична енергія

Кінетичною енергією матеріальної точки називається скалярна величина, що дорівнює половині добутку її маси на квадрат швидкості точки:

.

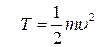(33.32)

З визначення кінетичної енергії виходить, що вона є скалярною додатною величиною; одиниця її вимірювання 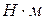або .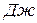

Кінетичною енергією механічної системи називають суму кінетичних енергій всіх точок цієї системи:

.

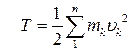(33.33)

При поступальному русі твердого тіла миттєві швидкості всіх його точок однакові і дорівнюють швидкості 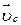центра мас тіла. Тому формула (33.33) набуває вигляду:

,

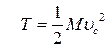(33.34)

де - маса тіла.

При обертанні тіла навколо нерухомої осі (наприклад, осі 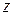) лінійна швидкість 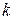-ї точки тіла 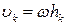, де 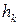- відстань точки до осі обертання. Тоді:

,

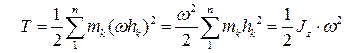(33.35)

оскільки 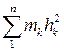- момент інерції 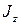тіла навколо осі обертання.

Плоскопаралельний рух тіла можна розглядати як миттєвообертальний навколо осі, що проходить через МЦШ Р. Отже, на підставі (33.34), отримаємо:

,

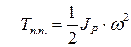(33.36)

де 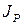- момент інерції тіла навколо осі, що проходить через МЦШ.

Але користування формулою не завжди зручно, бо положення миттєвого центра швидкостей при русі тіла змінюється і величина 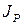також буде змінною.

За теоремою Гюйгенса:

,

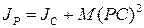де: 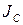- момент інерції тіла відносно осі, яка проходить через центр мас С тіла паралельно до миттєвої осі обертання. Крім того, якщо швидкість центра мас тіла 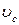виразити через добуток кутової швидкості тіла на відстань центра мас до МЦШ - 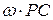, то (33.36) набуває вигляду:

.

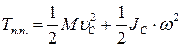(33.36)

Тобто, кінетична енергія тіла при плоскопаралельному русі складається з енергії поступального руху зі швидкістю центра мас і енергії обертального руху навколо центра мас.