Обчислення осьових моментів інерції деяких однорідних тіл

1. Тонкий однорідний стержень довжиною 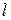і масою .

Підрахуємо момент інерції стержня відносно осі 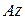, що проходить через його кінець 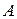перпендикулярно до осі стержня. Координатну вісь 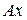направляємо вздовж 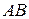(рис.а).

Оскільки стержень однорідний, то маса елементарного відрізка довжиною 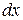, який знаходиться на відстані від осі , .

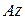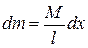Тоді згідно з формулою (3.50'):

.

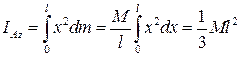Рис. а

2. Тонке однорідне кільце маси М і радіуса R.

Визначимо момент інерції кільця відносно осі 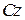, що проходить через його центр мас С перпендикулярно до площини кільця (рис. б). Так як всі елементарні маси кільця знаходяться на однаковій відстані R від осі Сz, то:

РРис. б

1. Кругла однорідна пластина чи циліндр радіуса R і маси M.

Підрахуємо момент інерції круглої пластини відносно осі 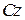, перпендикулярної до пластини (рис. в). Площа елементарного кільця радіуса 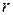і шириною 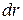дорівнює 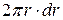. Маса одиниці площі 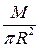. Тоді маса елементарного кільця 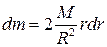, а момент інерції .

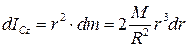Для всієї пластини :

.

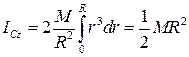Момент інерції для однорідного круглого циліндра масою М і радіусом R відносно його поздовжньої центральної осі (рис. г) буде визначатися такою ж формулою.