Теореми про зміну кінетичної енергії

Для матеріальної точки масою 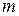, що рухається під дією сили 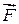, основне рівняння динаміки має вигляд:

.

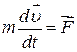Помножимо обидві частини цього співвідношення скалярно на :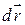

,

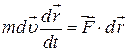звідкіля

.

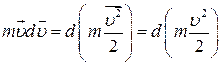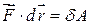Так як і , то:

.

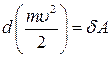(33.37)

Формула (33.37) є математичним записом теореми про зміну кінетичної енергії матеріальної точки в диференціальній формі: диференціал кінетичної енергії матеріальної точки дорівнює елементарній роботі сили, що діє на цю точку.

Якщо обидві частини (33.37) поділити на 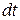, то отримаємо рівняння

,

(33.38)

з якого виходить, що похідна за часом від кінетичної енергії точки дорівнює потужності сили, прикладеної до цієї точки.

Проінтегруємо обидві частини рівняння (33.38) в межах, відповідних значенням величин при початковому 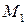і кінцевому 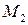положеннях рухомої точки, і знаходимо:

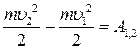
(33.39)

або

.

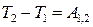(33.39')

Отже, зміна кінетичної енергії матеріальної точки на деякому її переміщенні дорівнює сумі робіт прикладених до неї сил на тому ж переміщенні.

Розглянемо механічну систему, що складається з 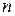матеріальних точок 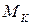масою 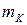кожна, і яка рухається відносно нерухомої системи відліку. Прикладемо до точок системи зовнішні і внутрішні сили. Тоді для 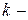ї точки теорема про зміну кінетичної енергії приймає вигляд:

,

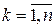або

.

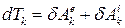Підсумуємо ці рівняння по всіх 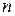точках системи:

.

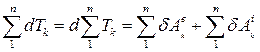Рахуючи, що 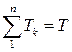- кінетична енергія системи, а 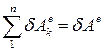, , 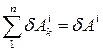де 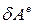, 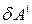- елементарні роботи всіх зовнішніх і всіх внутрішніх сил відповідно, отримаємо:

.

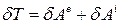(33.40)

Таким чином диференціал кінетичної енергії матеріальної системи дорівнює сумі елементарних робіт всіх зовнішніх та внутрішніх сил, що діють на систему.

Інтегруючи вираз (33.40), отримаємо математичну інтерпретацію теореми в інтегральній формі:

.

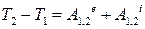(33.41)

де 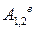, 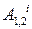- відповідно повні роботи зовнішніх і внутрішніх сил на скінченому переміщенні 1-2 системи.

Отже, зміна (приріст) кінетичної енергії системи при переході її з одного положення в інше дорівнює сумі робіт всіх зовнішніх і внутрішніх сил, що діють на систему на даному переміщенні.

Частинний випадок.

Для абсолютно твердого тіла сума робіт всіх внутрішніх сил системи дорівнює нулю. Тому теорема про зміну кінетичної енергії твердого тіла набуває вигляду:

.

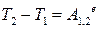(33.42)

Треба мати на увазі, що, на відміну від розглянутих нами інших загальних теорем динаміки системи, до теореми кінетичної енергії можуть входити внутрішні сили.

[1] Стичною площиною в точці М траєкторії називають граничне положення площини, проведеної через дотичну до траєкторії в точці М паралельно суміжній дотичній в точці М₁, коли остяння прагне збігтися з точкою М (рис.21.4)

1 Ф.Грасгоф (1826…1893) – німецький механік і машинобудівник.