Моментом кількості руху матеріальної точки відносно нерухомого центра О називається векторний добуток радіуса-вектора точки на кількість її руху .

Згідно з рис.33.1 момент кількості руху точки:

.

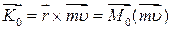(33.17)

Рис.33.1

Модуль момента кількості руху:

.

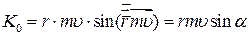(33.18)

Напрям кінетичного момента визначається за правилом векторного добутку двох векторів.

Аналогічно поняттю момента сили відносно осі визначається і момент кількості руху матеріальної точки відносно нерухомої осі. Так, відносно осі 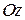(рис.33.1) кінетичний момент (величина скалярна) визначається за формулою:

,

(33.19)

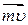де - перпендикуляр, опущений з точки О на лінію дії проекції кількості руху на площину .

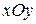В системі одиниць СІ модуль кінетичного момента вимірюється 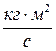в або в .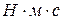

Кінетичним моментоммеханічної системи відносно центра О називається векторна величина , яка дорівнює геометричній сумі моментів кількостей рухів всіх матеріальних точок системи відносно того ж центра:

.

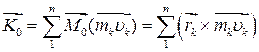(33.20)

Кінетичний момент системи як вектор, прикладений до центра О відносно якого він визначається.

Кінетичні моменти механічної системи відносно декартових координатних осей є проекціями вектора на ці осі:

.

(33.21)