Маса і центр мас системи
Механічна система як об’єкт дослідження характеризується своєю масою і центром мас.
Масою системи, що складається з «n» матеріальних точок, називається величина М, яка дорівнює сумі мас усіх точок:
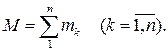
| (32.2) |
Центром мас (центром інерції) матеріальної системи називається геометрична точка С, радіус-вектор  якої визначається рівнянням:
якої визначається рівнянням:
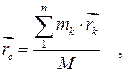
| (32.3) |
де: 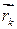 - радіус-вектор
- радіус-вектор 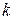 -ї точки;
-ї точки;  - маса цієї точки.
- маса цієї точки.

Рис.32.1
Координати центра мас в декартовій системі відліку дорівнюють (рис.32.1):
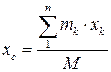 ; ;
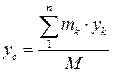 ; ;
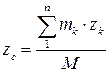 . .
| (32.4) |
В цих формулах 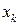 ,
, 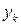 ,
, 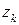 - координати k-ї точки.
- координати k-ї точки.
При неперервному розподілу мас в механічній системі, наприклад, коли система являє собою суцільне тверде тіло, суми, що стоять у правих частинах формул (32.3) і (32.4), переходять у відповідні інтеграли.
Моменти інерції
При дослідженні рухів механічної системи недостатньо знати її масу і положення центра мас. Для характеристики розподілу мас в системах, елементи яких беруть участь в обертальному русі, вводять поняття момента інерції. Розрізняють моменти інерції відносно довільного центра (полярний момент інерції), відносно осі (осьовий момент інерції), відносно площини (планарний момент інерції), а також відцентрові моменти інерції.
Полярним моментом інерції механічної системи, що складається з «n» матеріальних точок, відносно деякого центра О називається сума добутків мас точок системи на квадрати їх відстаней від цього центра (рис.32.2):
| (32.5) |
 Моментом інерції системи відносно довільної осі (наприклад, осі Оz рис.32.2) називають суму добутків мас кожної точки системи на квадрати їх відстаней до цієї осі:
Моментом інерції системи відносно довільної осі (наприклад, осі Оz рис.32.2) називають суму добутків мас кожної точки системи на квадрати їх відстаней до цієї осі:
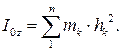
| (32.6) |
Для суцільних твердих тіл формули (3.49) і (3.50) набувають,  відповідно, вигляду:
відповідно, вигляду:
Рис. 32.2
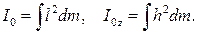
| (32.6') |
Радіус інерції. В техніці дуже часто для визначення момента інерції деталей (тіл) складної форми користуються поняттям радіуса інерції цих тіл.
Радіусом інерції тіла відносно даної осі називають відстань 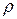 від осі до такої точки, в якій потрібно зосередити масу всього тіла, щоб момент інерції однієї цієї точки дорівнював моменту інерції тіла відносно тієї ж осі:
від осі до такої точки, в якій потрібно зосередити масу всього тіла, щоб момент інерції однієї цієї точки дорівнював моменту інерції тіла відносно тієї ж осі:
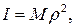
| (32.7) |
звідкіля:
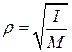
| (32.8) |
Планарним моментом інерції називають скалярну величину, яка дорівнює сумі добутків маси кожної точки системи на квадрат відстані цієї точки до певної площини.
Так, коли матеріальна система розглядається в декартовій системі координат (рис.32.2), то її моменти інерції відносно площин 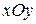 ,
, 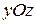 і
і 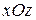 відповідно будуть дорівнювати:
відповідно будуть дорівнювати:
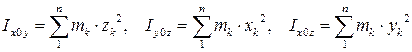
| (32.9) |
Крім осьових і полярних моментів інерції, при розв’язанні деяких задач динаміки (наприклад, в теорії зрівноважування роторів) користуються відцентровими моментами інерції (ВМІ).
Відцентровим моментом інерції механічної системи називають величину, яка дорівнює сумі добутків маси кожної точки системи на дві її координати, тобто:
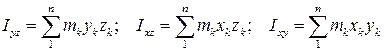
| (32.10) |
Відцентрові моменти інерції залежать не тільки від напряму координатних осей, а і від вибору початку координат. Тому, коли іде мова про відцентровий момент інерції у певній точці, то під цим розуміють, що початок координат співпадає з цією точкою.
На відміну від осьових, відцентрові моменти інерції можуть бути додатними від’ємними або перетворюватись на нуль.
Якщо два ВМІ, що містять у своїх індексах знак певної координатної осі, дорівнюють нулю, то ця вісь називається головною віссю інерції механічної системи або тіла в даній точці. Наприклад, якщо 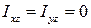 , то вісь
, то вісь 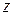 є головною віссю інерції. Якщо до того ця вісь проходить через центр мас тіла (системи), то вона називається головною центральною віссю інерції.
є головною віссю інерції. Якщо до того ця вісь проходить через центр мас тіла (системи), то вона називається головною центральною віссю інерції.
Слід відмітити два частинних випадки, коли зразу можна визначити характер осі:
- Якщо тіло має площину матеріальної симетрії, то для всіх її точок вісь, перпендикулярна до площини симетрії, є головною віссю інерції.
- Якщо тіло (матеріальна система) має вісь матеріальної симетрії, то ця вісь є головною центральною віссю інерції, і її часто називають віссю динамічної симетрії.
Теорема Гюйгенса
Моменти інерції даного тіла відносно різних осей будуть мати різні значення. Залежність між моментами інерції тіла відносно двох паралельних осей визначається теоремою Гюйгенса:
момент інерції механічної системи (твердого тіла) відносно будь-якої осі дорівнює сумі момента інерції відносно осі, що проходить через центр мас цієї системи (тіла) паралельно даній, і добутку маси системи на квадрат відстані між цими осями.
Припустимо, що відомий момент інерції тіла відносно осі 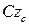 , яка проходить через центр мас
, яка проходить через центр мас 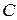 тіла. Визначимо момент інерції цього тіла відносно осі
тіла. Визначимо момент інерції цього тіла відносно осі 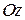 , проведеної паралельно до
, проведеної паралельно до 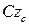 на відстані «d» від неї (рис.3.15). Оберемо довільну точку К тіла масою
на відстані «d» від неї (рис.3.15). Оберемо довільну точку К тіла масою  , яка відстоїть від центральної осі
, яка відстоїть від центральної осі 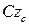 на відстані
на відстані 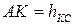 і на відстані
і на відстані 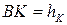 - від осі
- від осі 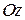 .
.

|
| Рис. 32.3 |
Утворений трикутник 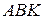 з кутом
з кутом 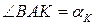 буде паралельним площині
буде паралельним площині 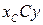 (а також
(а також 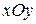 ).
).
З трикутника за теоремою косинусів отримаємо:
 Помножимо кожний член цього співвідношення на масу
Помножимо кожний член цього співвідношення на масу 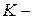 ї точки
ї точки  і просумуємо по всіх точках тіла:
і просумуємо по всіх точках тіла:

Оскільки:
 і
і  , то:
, то:
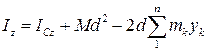 .
.
Але 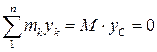 , бо в нашому випадку координата центра мас тіла
, бо в нашому випадку координата центра мас тіла 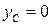 .
.
Таким чином, кінцево маємо:
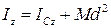 , ,
| (32.11) |
що і потрібно було довести.
Дата добавления: 2016-01-26; просмотров: 1657;
