Механічна система і сили, що діють на її складові

Моделювання реального тіла як матеріальної точки має певні обмеження (це ті випадки, коли розмірами тіл згідно з умовою задачі можна знехтувати). Проте часто реальний об’єкт необхідно розглядати в якості механічної системи, тобто сукупності матеріальних точок або тіл, в якій положення і рух кожної точки (тіла) залежить від положення і руху всіх інших. Ця залежність обумовлена силовою взаємодією між окремими елементами механічної системи.

В курсі статики ми поділяли всі сили, прикладені до твердого тіла чи системи тіл, на активні і реакції в’язей, розуміючи під першими сили, що не залежать від в’язей. Там же було показано, що сили можна також поділити на зовнішні і внутрішні.

Нагадаємо ще раз визначення зовнішніх і внутрішніх сил. Зовнішніми називають сили, які є результатом дії на точки (тіла) даної механічної системи з боку тіл, що не входять до складу цієї системи. Сили взаємодії між матеріальними точками чи тілами системи називають внутрішніми. Позначаються зовнішні сили верхнім індексом 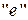, а внутрішні – верхнім індексом (від початкових літер французьких слів exerieur – зовнішній і interieur – внутрішній):

- зовнішня сила, 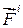- внутрішня сила.

Властивості внутрішніх сил виходять з третього закону Ньютона і зводяться д наступного:

Геометричні суми всіх внутрішніх сил механічної системи і їх моментів відносно довільного центра простору дорівнюють нулю при будь-якому стані системи. Тобто:

.

(32.1)

Рівність нулю головного вектора і головного момента внутрішніх сил зовсім не означає, що ці сили зрівноважені. Слід пам’ятати, що внутрішні сили прикладені до різних тіл даної матеріальної системи, які в загальному випадку можуть переміщуватись одне відносно другого. Прикладом може бути Сонячна система, планети якої і їх супутники здійснюють складні рухи під дією тільки внутрішніх сил.