Наращенная сумма постоянной ренты постнумерандо
Методом прямого счета можно найти наращенную сумму и современную стоимость любого потока платежей, в том числе и постоянной ренты. Однако удобнее, особенно в аналитических целях, воспользоваться более компактными формулами. Поскольку обобщающие характеристики постоянных рент играют существенную роль в анализе финансовых операций, получим эти формулы для всех видов постоянных рент.
Годовая рента.Начнем с наиболее простого случая - годовой ренты постнумерандо. Пусть в течение п лет в банк в конце каждого года вносится по R рублей. На взносы начисляются сложные проценты по ставке i. Таким образом, имеется рента, член которой равен R , а срок - п. Все члены ренты, кроме последнего, приносят проценты - на первый член проценты начисляются п - 1 год, на второй п - 2и т.д. На последний взнос проценты не начисляются (напомним, что рента постнумерандо). Наращенная к концу срока каждого взноса сумма составит:
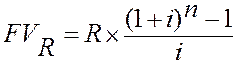 .
.
Пример: Создается фонд посредством ежегодных взносов по 10 тыс. $ в течение шести лет. На собранные средства банк начисляет проценты по ставке 15% годовых. Определить размер фонда к концу шестого года.
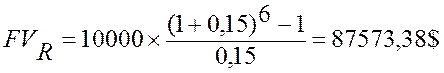 .
.
Годовая рента, начисление процентов m раз в году. Пусть, как и выше, анализируется годовая рента постнумерандо. Однако проценты теперь начисляются m раз в году. Число членов ренты равно n.
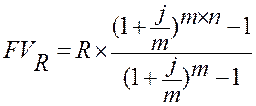
где j – номинальная ставка процентов.
множители: 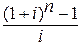 и
и 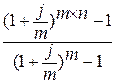 называются коэффициентами наращения ренты.
называются коэффициентами наращения ренты.
Пример: Предположим, что при условиях, изложенных в предыдущем примере, проценты капитализируются поквартально, тогда:
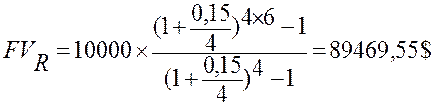 .
.
Как видим, переход от годового начисления процентов к квартальному несколько увеличил наращенную сумму.
Рассмотрим теперь методы расчета наращенной суммы для вариантов р-срочной ренты постнумерандо при условии, что m =1, m = p и m ≠ p.
Рента р-срочная (m = 1).Пусть рента выплачивается р раз в году равными суммами, процент начисляется раз в конце года. Если годовая сумма платежей равна R, то каждый раз выплачивается R/p. Общее число членов ренты равно np.
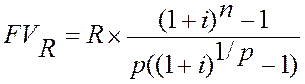 .
.
Пример: Вернемся к первому примеру. Допустим, платежи выплачиваются поквартально: R/p=2,5 тыс. $., общее число платежей равно 24. Наращенная сумма составит
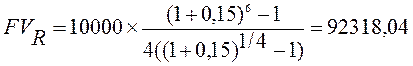 $.
$.
Рента р-срочная (m = р).На практике наиболее часто встречаются случаи, когда число выплат в году равно числу начислений процентов: m = p. В этом случае наращенная сумма ренты составит:
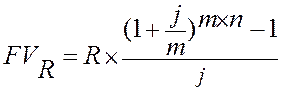 .
.
Пример: Продолжим наш сквозной пример. Пусть выплата членов ренты и начисление процентов производится поквартально. Тогда:
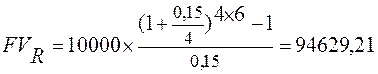 $.
$.
Рента р-срочная(m ≠ p). Определим теперь наращенную сумму для наиболее общего случая – р-срочная рента с начислением процентов m раз в году. Общее количество членов ренты равно np, величина члена ренты R/p. наращенная сумма такой ренты составит:
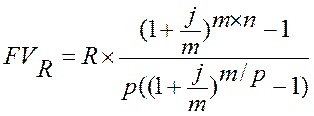 .
.
Пример: Если в ренте, наращенная сумма которой определялась в предыдущем примере, начисление процентов производится ежемесячно, то
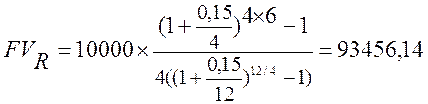 $.
$.
Непрерывное начисление процентов. В целой области финансовых расчетов, главным образом это касается финансового анализа, целесообразно воспользоваться методом наращения ренты с помощью непрерывных процентов. При дискретном потоке платежей общая формула выглядит следующим образом:
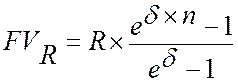 ,
,
d - где непрерывная сложная процентная ставка,
е – основание натуральных логарифмов.
Аналогично для р-срочной ренты находим
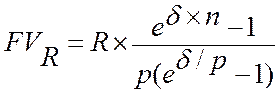 .
.
Пример: Используя данные вышеназванных примеров, наращенную сумму фонда определим с помощью непрерывных процентов.
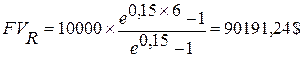 .
.
При ежеквартальной выплате членов ренты получим
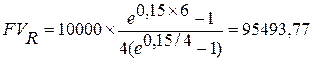 $.
$.
Дата добавления: 2016-01-20; просмотров: 2957;
