Непрерывные проценты
В практически финансово-кредитных операциях непрерывное наращение, т.е. наращение за бесконечно малые отрезки времени, применяется крайне редко. Существенно большее значение непрерывное наращение имеет в анализе сложных финансовых проблем, например, при обосновании и выборе инвестиционных решений, в финансовом проектировании.
При непрерывном наращении процентов применяют особый вид процентной ставки – силу роста.
Сила роста характеризует относительный прирост наращенной суммы за бесконечно малый промежуток времени. Она может быть постоянной или изменяться во времени.
Для того чтобы отличить непрерывную ставку от дискретной, обозначим силу роста как δ. Тогда наращенная сумма по непрерывной ставке составит:
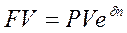 .
.
Дискретные и непрерывные ставки наращения находятся в функциональной зависимости. Из равенства множителей наращения
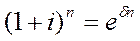 следует:
следует: 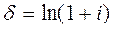 ,
,
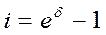 .
.
Пример: Сумма, на которую начисляются непрерывные проценты, равна 2 млн. руб., сила роста 10%, срок 5 лет. Определить наращенную сумму.
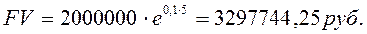
Непрерывное наращение по ставке = 10% равнозначно наращению за тот же срок дискретных сложных процентов по годовой ставке:
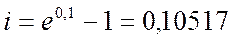
В итоге получим:
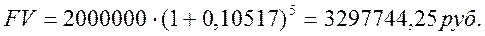
Формула дисконтирования:
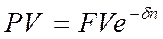 .
.
Дисконтный множитель равен 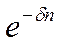 .
.
Пример: Определить современную стоимость платежа, если наращенная стоимость равна 5000 тыс. руб. при условии дисконтирования по силе роста 12%. Срок платежа – 5 лет.
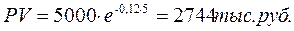
Срок ссуды при постоянной силе роста:
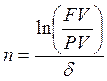 .
.
Сила роста:
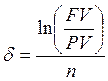 .
.
Дата добавления: 2016-01-20; просмотров: 1873;
