Виды потоков платежей и их основные параметры

Современные финансово-банковские операции часто пред­полагают не отдельные или разовые платежи, а некоторую их последовательность во времени, например, погашение задол­женности в рассрочку, периодическое поступление доходов от инвестиций, выплаты пенсии и т. д. Такого рода последователь­ность, или ряд платежей, называют потоком платежей. (В западной финансовой литературе в аналогичном смысле приме­няется термин cash flows stream - буквально, потоки налично­сти, хотя речь идет о потоке денег в любом виде.) Отдельный элемент такого ряда платежей назовем членом потока (cash flow). Введение понятия поток платежей в финансовый количественный анализ, что произошло сравнительно недавно, за­метно расширило рамки и возможности последнего.

Классификация потоков.В практике встречаются разнообраз­ные потоки платежей. Причем один и тот же вид потока может быть использован в анализе различных финансово-кредитных операций.

Потоки платежей могут быть регулярными(размеры платежей постоянные или следуют установленному правилу, предусмат­ривающему равные интервалы между платежами) и нерегулярны­ми. Члены потоков могут быть как положительными (поступле­ния), так и отрицательными величинами (выплаты).

Поток платежей, все члены которого - положительные ве­личины, а временные интервалы между платежами одинаковы, называют финансовой рентой,или просто рентой (rent). Напри­мер, рентой является последовательность получения процентов по облигации, платежи по потребительскому кредиту, выплаты в рассрочку страховых премий и т.д. Иногда подобного рода по­ток платежей называют аннуитетом (annuity), что, строго гово­ря, применимо только к ежегодным выплатам.

Использование в финансово-банковской операции условий, предполагающих выплаты в виде финансовой ренты, сущест­венно упрощает количественный их анализ, дает возможность применять стандартные формулы и таблицы значений многих, необходимых для финансовых расчетов коэффициентов.

Рента описывается следующими параметрами:

член ренты (rent) - размер отдельного платежа;

период ренты (rent period, payment period) - временной интервал между двумя последова­тельными платежами;

срок ренты (term) - время от начала пер­вого периода ренты до конца последнего;

процентная ставка. Размер ставки не всегда прямо оговаривается в условиях фи­нансовой операции. Однако, этот параметр крайне необходим для ее анализа.

При характеристике некоторых видов рент необходимо указать дополнительные ус­ловия и параметры. Например, число платежей в году, способ и частота начислений процентов, параметры, характеризующие закономерность изменения размеров члена ренты во времени.

В практике применяют разные по своим условиям ренты. В основу их классификации может быть положен ряд признаков. Рассмотрим некоторые из таких классификаций.

1. По количеству выплат членов ренты на протяжении года ренты делятся на годовые (выплата раз в году) и р-срочные (р - количество выплат в году). В анализе производственных инве­стиций иногда применяют ренты с периодами, превышающими год. Перечисленные виды рент называют дискретными. В фи­нансовой практике встречаются и с такими последовательно­стями платежей, которые производятся так часто, что их практически можно рассматривать как непрерывные.

2. По числу раз начислений процентов на протяжении года различают: ренты с ежегодным начислением, с начислением т раз в году, с непрерывным начислением. Моменты начисления процентов необязательно совпадают с моментами выплат чле­нов ренты. Однако, расчеты заметно упро­щаются, если два указанных момента совпадают.

3. По величине своих членов ренты делятся на постоянные (с одинаковыми размерами члена ренты) и переменные. Члены переменных рент изменяют свои размеры во времени, следуя ка­кому-либо закону, например арифметической или геометриче­ской прогрессии, или несистематично (задаются таблицей). По­стоянные ренты - наиболее распространенный вид ренты.

4. По вероятности выплат ренты делятся на верные (annuity cer­tain) и условные (contingent annuity). Верные ренты подлежат без­условной уплате, например, при погашении кредита. Число членов такой ренты заранее известно. В свою очередь выплата условной ренты ставится в зависимость от наступления некото­рого случайного события, число ее членов заранее неизвестно. К такого рода рентам относятся страховые аннуитеты - последовательные платежи в имущественном и личном страхова­нии. Типичным примером страхового аннуитета является по­жизненная выплата пенсии.

5. По количеству членов различают ренты с конечным числом членов, или ограниченные ренты (их срок заранее оговорен), и бесконечные, или вечные ренты (perpetuity). С вечной рентой встречаются на практике в ряде долгосрочных операций, когда предполагается, что период функционирования анализируемой системы или срок операции весьма продолжителен и не огова­ривается конкретными датами. В качестве вечной ренты логич­но рассматривать и выплаты процентов по бессрочным облига­ционным займам.

6. По соотношению начала срока ренты и какого-либо момен­та времени, упреждающего начало ренты (например, начало действия контракта или даты его заключения), ренты делятся на немедленные и отложенные, или отсроченные (deffered annu­ity). Пример отсроченной ренты: погашение долга в рассрочку после льготного периода.

7. По моменту выплат плате­жей в пределах периода ренты. Если платежи осуществляются в конце этих периодов, то соответствующие ренты называют обыкновенными, или постнумерандо (ordinary annuity), если же платежи производятся в начале периодов, то их называют пренумерандо (annuity due). Иногда контракты предусматривают платежи или поступления денег в середине периодов.

Приведем пример. Контракт предусматривает периодическое погашение задолженности путем выплаты в конце каждого по­лугодия одинаковых погасительных платежей на протяжении фиксированного числа лет, Таким образом, предусматривается постоянная, полугодовая, верная, ограниченная рента постну­мерандо.

Обобщающие параметры потоков платежей. Вподавляющем числе практических случаев анализ потока платежей предпола­гает расчет одной из двух обобщающих характеристик: нара­щенной суммы или современной стоимости потока.

Наращен­ная сумма (amount of cash flows) - сумма всех членов потока пла­тежей с начисленными на них к концу срока процентами.

Современная стоимость потока платежей (present value of cash flows) - это сумма всех его членов, дисконтированных на начало срока ренты или некоторый упреждающий момент вре­мени. Конкретный смысл этих характеристик определяется со­держанием его членов или их происхождением. Наращенная сумма может представлять собой общую сумму накопленной задолженности к концу срока, итоговый объем инвестиций, на­копленный денежный резерв и т. д. В свою очередь современ­ная стоимость характеризует приведенные к началу осуществле­ния проекта инвестиционные затраты, суммарный капитализи­рованный доход или чистую приведенную прибыль от реализа­ции проекта и т. п.

Обобщающие поток платежей характеристики, особенно его современная стоимость, широко применяются в различных фи­нансовых расчетах. Так, без них, например, невозможно разра­ботать план последовательного погашения задолженности, из­мерить финансовую эффективность проекта, осуществить срав­нение или безубыточное изменение условий контрактов, ре­шать многие другие практические задачи

Прямой метод расчета наращенной суммы и современной сто­имости потока платежей.Рассмотрим общую постановку задачи. Допустим, имеется ряд платежей R_t, выплачиваемых спустя вре­мя n_t, после некоторого начального момента времени. Общий срок выплат п лет. Необходимо определить наращенную на ко­нец срока потока платежей сумму. Если проценты начисляют­ся раз в году по сложной ставке i, то, обозначив искомую вели­чину через FV_R, получим по определению

.

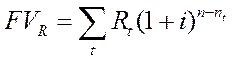Современную стоимость такого потока также находим пря­мым счетом как сумму дисконтированных платежей:

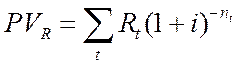
где PV_R - современная стоимость потока платежей.

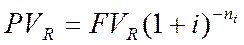
Пример: График предусматривает следующий порядок вы­дачи ссуды во времени: 1 июля 2005 г. - 5 млн. руб., 1 января 2006 г. - 15 млн. руб., 1 января 2008 г. - 18 млн. руб. Необходи­мо определить сумму задолженности на начало 2009 г. при усло­вии, что проценты начисляются по ставке 20%. Схематично усло­вия задачи показаны на рисунке.

5 15 18 FV_R = ?

1 июля 1 января 1 января 1 января t.

2005 г. 2006 г. 2008 г 2009 г.

Находим FV_R = 5 ×1,2^3,5 + 15 ×1,2³ + 18 × 1,2¹ = 56,985 млн. руб.

По этим же данным определим современную стоимость пото­ка на момент выплаты первой суммы. При прямом счете получим

PV_R = 5 + 15 ×1,2^-0,5 + 18 × 1,2^-2,5= 30,104 млн . руб.

PV_R = 56,985 × 1,2^-3,5= 30,104 млн. руб.