На сумму 6 тыс. руб. в течение 5 лет начисляются непрерывные проценты. Определите наращенную сумму и процентный доход, если сила роста равна 12%.

Решение:

Поскольку Р = 6 тыс. руб., r = 0,12 и п = 5, получим

F₅ = 6 * e ^0,12*5 = 6 * 2,78 ^0,6 = 6 * ⁵ 2,78 ³ = 6*1,88 = 11,28 (тыс. руб.),

и поэтому процентный доход составит величину I = 11,28 – 6 = 5.28 (тыс. руб.).

Капитал в размере 3000 рублей вложен на 6 лет под 6% годовых. Найти доход от вложения денег при декурсивном и антисипативном способе расчета сложных процентов.

Решение:

F₆ = P * (1+r)ⁿ = 3000*(1+0,06)⁶ = 3000*1,4185 = 4255,56

I = 4255,56 – 3000 = 1255,56

Это при декурсивном способе расчета

F₆ = P * (1/(1-r))ⁿ = 3000*(1/(1-0,06))⁶ = 3000*1,4495 = 4348,65

I = 4348,65 – 3000 = 1348,65

Данный пример показывает, что при антисипативном расчете получается больший доход

В банк вложено 20000 руб. под 6% годовых. Используется декурсивный способ расчета. Требуется найти конечную сумму капитала через 10 лет при годовой и полугодовой капитализации.

Решение:

F₁₀ = P * (1+r)ⁿ = 20000*(1+0,06)¹⁰ = 20000*1,7908 = 35816,95

F₂₀ = P * (1+r)ⁿ = 20000*(1+0,06/2)²⁰ = 20000*1,8061 = 36122,22

Вклад в сумме 2000 руб. внесен в банк под 40% годовых. Сколько денег должны выплатить клиенту банка через 6 месяцев при использовании схемы сложных и простых процентов? Какую сумму можно получить через 1,5 года при смешанной схеме начисления процентов, при начислении сложных процентов, при начислении простых процентов ?

Решение:

F_1/2 = P * (1+r)ⁿ = 2000*(1+0,40)^1/2 = 2000*1,1832 = 2366,43 –это при схеме сложных процентов

F = P*(1+nr) = 2000*(1+1/2*0,40) = 2400 – это при начислении простых процентов

Если вклад будет изъят через 1,5года то смешанная схема начисления даст следующий результат:

F_1,5 = P * (1+r)^w * (1+f*r) = 2000 * (1+0,40)¹ * (1+1/2*0,40) = 3360

При расчете только по сложным процентам получим:

F_1,5 = P * (1+r)ⁿ = 2000*(1+0,40)^1,5 = 2000*1,4*1,4 ^½ = 3313

При расчете по простым процентам:

F = P*(1+nr) = 2000*(1+3/2*0,40) = 3200

Известно, что кредитор при погашении кредита заемщиком получил 300 000 руб. Сумма кредита составляла 100 000 руб. и этот кредит был предоставлен на 2,5 года. Найти сложный годовой процент по этому кредиту.

Решение:

r = 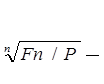1 = 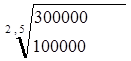- 1 = 3 ^2/5 – 1 = 9 ^1/5 –1 = 1,552 –1 = 0,552= 55,2%

Тема 5.6. Методы погашения (амортизации) займа (кредита)

Амортизация займа выражается в постепенном погашении кредита путем периодических взносов по заранее утвержденному плану погашения.

Существуют следующие способы амортизации займа: