Интегрирующее и дифференцирующее звенья

Интегрирующее звено имеет передаточную функцию К(р) = К / р. Переходная характеристика такого звена: h(t)=α t, где α = arctg K (рис. 7.2, а).

АФ Х интегрирующего звена имеет вид:

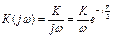
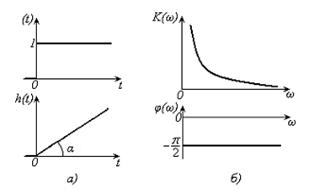
Рис. 13.6 – Характеристики интегрирующего звена: а) переходная характеристика; б) частотные характеристики

Примеры такого звена: конденсатор, для которого входной величиной является ток, выходной – напряжение; бункер для зерна; электрический двигатель, если входная величина угловая скорость, выходная - угол поворота ротора и др.

Для интегрирующего звена входная величина х и выходная у связаны зависимостью:

.

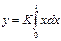Дифференцирующее звено (идеальное) обладает передаточной характеристикой вида К(р) = К·р, а переходной характеристикой в виде дельта-импульса - 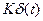. Для реального дифференцирующего звена передаточная функция имеет вид:

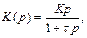
где К – коэффициент передачи; 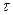- постоянная времени, характеризующая инерционные свойства звена.

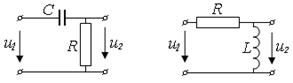
Удобными для анализа моделями дифференцирующего звена являются звенья, состоящие из RС- и RL – элементов (Рис.13.7). Для них τ = RС или τ = L / R .

Примером дифференцирующего звена является датчик угловой скорости – тахогенератор.

Рис.13.7 – Модели дифференцирующего звена

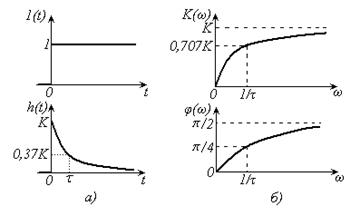
Переходная и частотные характеристики реального дифференцирующего звена приведены на рис. 13.8 а, б.

Рис. 13.8 – Характеристики реального дифференцирующего звена: а) переходная характеристика; б) частотные характеристики

Реальное интегрирующее звено (апериодическое звено первого порядка). Оно описывается линейным дифференциальным уравнением первого порядка:

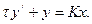
Если в качестве х принять сигнал 1(t), то получим переходную характеристику

h(t)=K(1-e^-t/τ).

Если в исходном линейном дифференциальном уравнении прейти к изображениям

; ,

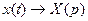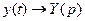то получим алгебраическое уравнение:

.

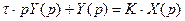Отсюда

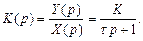
АФХ получим при р = jω, тогда

.

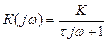Перейдя к алгебраической форме АФХ (умножив числитель и знаменатель на 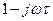), получим

.

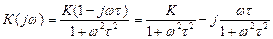Амплитудно-частотная характеристика (модуль К(jω))

,

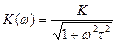фазочастотная характеристика (аргумент К(jω))

φ(ω) = – arctg(ωτ).

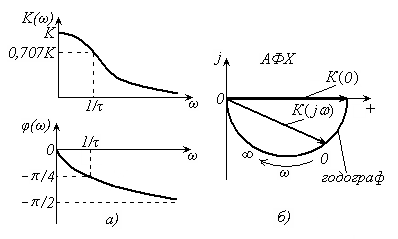
Графические изображения частотных характеристик приведены на рис.13.9, а. На рис. 13.9, б показан вид АФХ рассматриваемого звена, изображенной на комплексной плоскости.

Годографом называют линию, описываемую концом вектора 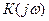на комплексной плоскости при изменении частоты ω от нуля до бесконечности. Как видно из рис. 7.5, б, годограф апериодического звена – полуокружность.

Моделями реального интегрирующего звена являются звенья, состоящие из RС- и RL-элементов (Рис.13.10). Для них х=и₁, у = и₂, τ = RС или τ = L / R .

Рис. 13.9 – Частотные характеристики апериодического звена первого порядка: а) АЧХ и ФЧХ; б) АФХ и годограф

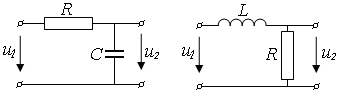
Рис. 13.10 – Модели реального интегрирующего звена