Автоматические системы и регуляторы

Задача автоматического регулирования

Основной задачей автоматического регулирования является поддержание определенного закона изменения одной или нескольких физических величин в регулируемом (управляемом) объекте. В зависимости от структуры объекта различают задачи одноканального и многоканального управления.

Одноканальные задачи управления, к которым относятся задачи стабилизации, слежения и терминального управления, когда выходная переменная y(t) является скалярной функцией времени, устанавливают желаемый характер изменения переменных объекта управления.

Задача стабилизации или регулирования формулируется как задача поддержания выходной переменной на заданном уровне у_зад = const при t → ∞.

Задача слежения - это задача соблюдения заданного закона y*(t) изменения параметра у(t), то есть y(t) → у*(t), при t → ∞. Здесь различают:

- задачи слежения за внешним объектом, когда функция y*(t) является выходом внешнего объекта и заранее неизвестна;

- задачи программного управления, в которых программа движения y*(t) генерируется специальным задающим блоком (программатором), входящим в состав САУ.

Система автоматического управления, решающая задачу слежения, называется следящей системой. Сигнал y*(t), определяющий требуемый закон движения системы, называется задающим воздействием. Сигнал ∆y(t) = y*(t) – y(t), характеризующий текущее значение отклонения выходной переменной от задающего воздействия, называется рассогласованием, отклонением или ошибкой управления. Задачи стабилизации и слежения иначе могут быть сформулированы как задачи поддержания нулевого значения рассогласования, т. е. ∆y(t) → 0.

В многоканальных задачах управления выходом объекта служит векторная переменная (вектор выхода). Векторными переменными являются также задающие воздействие (вектор задания) и рассогласование (вектор ошибок). Формулировки основных задач многоканального управления практически не отличаются от одноканальных.

Математическое описание систем

И элементов автоматики

Описание систем и элементов автоматики в

Статическом режиме

Для создания автоматических систем необходимо иметь математическое описание (модель) процесса и математическую модель самой системы. За счет использования моделей во многом упрощаются решения поставленной задачи. Модель системы отображает определенные характеристики системы. При этом, наряду с аналитическими моделями используются и экспериментальные. Аналитические модели полнее отражают параметры объекта управления и системы, но и содержат ряд допущений и ограничений. Экспериментальные модели требуют минимальных сведений о процессах, но зачастую не удовлетворяют требованиям по точности инженерных расчетов.

По сути, математической моделью является совокупность уравнений и граничных условий, связывающих выходные и входные параметры САР и САУ, описывающих состояние этих систем в установившемся и переходном режимах.

Установившийся (статический) режим характеризуется состоянием, когда входные и выходные параметры системы постоянны во времени.

Для описания элементов и систем автоматики в статическом режиме используется статическая характеристика, выражающая зависимость выходной величины у элемента или системы от входной величины х в установившемся режиме, т. е. y = f(x). Эта зависимость является, как правило, нелинейной и ее не всегда удается аппроксимировать, т. е. описать аналитической функцией в целях дальнейшего анализа. В этих случаях используют ряд приемов и методов.

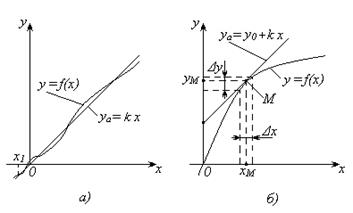
Метод осреднения, когда нелинейная характеристика – непрерывная функция на заданном участке ее изменения, заменяется некоторой, наиболее подходящей аналитической функцией, например, прямой линией (рис. 13.1, а).

Рис. 13.1 – Методы аппроксимации статических характеристик: а) метод осреднения; б) метод малых отклонений

Метод малых отклонений основан на замене нелинейной характеристики в окрестности рабочей точки М (x_м , y_м) прямой линией, касательной в этой точке (рис. 13.1, б). При этом рабочий диапазон элемента или системы Dx мал, а точка М находится в его середине. Аппроксимирующая функция в этом случае

у_а = y₀ + k x, где k = tgα, будет тем точнее отображать исходную зависимость y = f(x) в районе точки М, чем меньше участок Dx.

Метод выбранных точек основан на подборе аналитического выражения, например степенного многочлена, связывающего величины y и x при условии их совпадения в известных точках на статической характеристике: М₀ (x₀ , y₀); М₁ (x₁ , y₁) … М_n (x_n , y_n). При известных значениях координат точек (x₀ … x_n; y₀ … y_n), коэффициент многочлена находятся из системы уравнений:

y₀ = а₀ + а₁х₀ + …+ а_nx₀ⁿ;

y₁ = а₀ + а₁х₁ + …+ а_nx₁ⁿ;

…………………………………

y_n = а₀ + а₁х _n + …+ а_nx _n ⁿ.

Элементы и системы автоматики в статическом режиме характеризуются коэффициентом передачи, определяемым из статической характеристики, как

k=dy/dx.

Приближенно его определяют, как

К=Dy/Dx.

Для датчиков коэффициент К называют коэффициентом чувствительности, для усилителей – коэффициентом усиления.