Передаточная функция

,

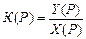где Y(P), X(P) – изображения по Лапласу функций y(t) и x(t).

Использование преобразований Лапласа лежит в основе операционного исчисления. Необходимость в нем возникает при анализе систем автоматики методом дифференциальных уравнений. Прямое преобразование Лапласа позволяет перейти от дифференциальных уравнений к алгебраическим за счет того, что операцию дифференцирования функций времени (оригиналов) можно заменить умножением их изображений на оператор р в соответствующей степени, тоесть

.

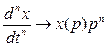При этом дифференциальные уравнения превращаются в алгебраические, которые легко решаются. От решений, полученных в операционной форме, с помощью обратного преобразования Лапласа (или по таблицам) находят оригиналы, например, функцию y(t). При известной передаточной функции системы, изображение Y(р) = К(р)× X(р), то есть легко определяется.

Формально, если в амплитудно-фазовой характеристике К(jω) заменить jω на оператор р, то также получим выражение для передаточной функции K(p).

Между функциями времени и их изображениями существуют предельные соотношения, которые полезны при проверке вычислений с помощью преобразований Лапласа.

Первое предельное соотношение:

_.

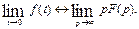Оно позволяет определить начальное значение функции f(t) при t = 0 непосредственно по изображению F(p).

Второе предельное соотношение:

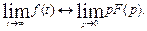
Оно дает возможность найти предел функции f(t) при t→ ∞ по значению ее изображения F(p) в начале координат при р = 0.